Question

(2006浙江，17)如下图，在四棱锥P－ABCD中，底面为直角梯形，AD∥BC，∠BAD=90°，PA⊥底面ABCD，且PA=AD=AB=2BC，M、N分别为PC、PB的中点．

(1)求证：PB⊥DM；

(2)求CD与平面ADMN所成的角．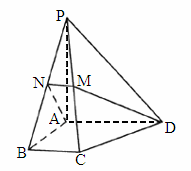

Answer 1

答案：略
解析：

解析：如图，以A为坐标原点建立空间直角坐标系A－xyz，设BC=1，则A(0，0，0)，P(0，0，2)，B(2，0，0)，C(2，1，0)，，D(0，2，0)． (1)因为， 所以PB⊥DM． (2)因为． 所以PB⊥AD， 又因为PB⊥DM， 所以PB⊥平面ADMN． 因为的余角即是CD与平面ADMN所成的角． 因此， 所以CD与平面ADMN所成的角为．