题目内容
已知a，b，m是正实数，且a＜b，求证：
＜
．
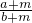证明：由a，b，m是正实数，故要证＜
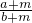
只要证a（b+m）＜b（a+m），只要证ab+am＜ab+bm，
只要证am＜bm，而m＞0，只要证 a＜b，
由条件a＜b成立，故原不等式成立．
分析：只要证a（b+m）＜b（a+m），只要证am＜bm，只要证 a＜b，而a＜b为已知条件，命题得证．
点评：本题主要考查不等式与不等关系，用分析法证明不等式，属于基础题．
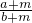
＜只要证a（b+m）＜b（a+m），只要证ab+am＜ab+bm，
只要证am＜bm，而m＞0，只要证 a＜b，
由条件a＜b成立，故原不等式成立．
分析：只要证a（b+m）＜b（a+m），只要证am＜bm，只要证 a＜b，而a＜b为已知条件，命题得证．
点评：本题主要考查不等式与不等关系，用分析法证明不等式，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，点A、B分别为双曲线C实轴的左端点和虚轴的上端点，点
、
分别为双曲线C的左、右焦点，点M、N是双曲线C的右支上不同两点，点Q为线段MN的中点．已知在双曲线C上存在一点P，使得
．
为正常数，若点Q在直线
上，求直线MN在y轴上的截距的取值范围. 
，点A、B分别为双曲线C实轴的左端点和虚轴的上端点，点F1、F2分别为双曲线C的左、右焦点，点M、N是双曲线C的右支上不同两点，点Q为线段MN的中点．已知在双曲线C上存在一点P，使得
．
，点A、B分别为双曲线C实轴的左端点和虚轴的上端点，点F1、F2分别为双曲线C的左、右焦点，点M、N是双曲线C的右支上不同两点，点Q为线段MN的中点．已知在双曲线C上存在一点P，使得
．