题目内容
(本题满分15分)四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G,F分别是线段CE,PB上的动点,且满足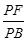 =
=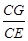 =λ∈(0,1).
=λ∈(0,1).
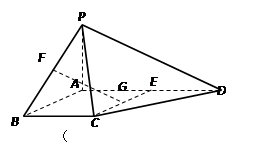
(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求λ的值,使得二面角F-CD-G的平面角的正切值为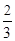 .
.
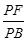 =
=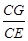 =λ∈(0,1).
=λ∈(0,1).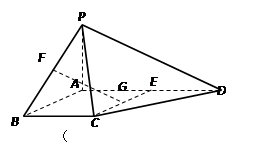
(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求λ的值,使得二面角F-CD-G的平面角的正切值为
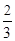 .
.方法一:
(Ⅰ) 证明:如图以点A为原点建立空间直角坐标系A-xyz,其中K为BC的中点,
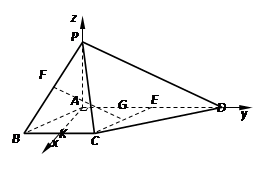
不妨设PA=2,则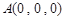 ,
,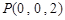 ,
,
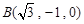 ,
,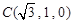 ,
,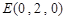 ,
,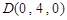 .
.
由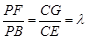 ,得
,得
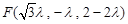 ,
,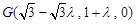 ,
,
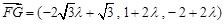 ,
,
设平面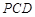 的法向量
的法向量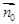 =(x,y,z),则
=(x,y,z),则
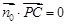 ,
,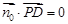 ,
,
得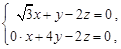
可取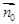 =(
=(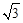 ,1,2),于是
,1,2),于是
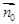
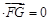 ,故
,故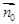
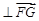 ,又因为FG
,又因为FG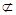 平面PDC,即
平面PDC,即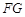 //平面
//平面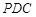 .
.
(Ⅱ) 解: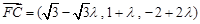 ,
,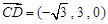 ,
,
设平面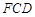 的法向量
的法向量 ,则
,则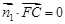 ,
,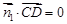 ,
,
可取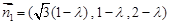 ,又
,又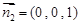 为平面
为平面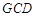 的法向量.
的法向量.
由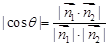 ,因为tan
,因为tan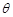 =
=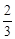 ,cos
,cos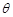 =
=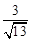 ,
,
所以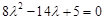 ,解得
,解得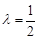 或
或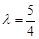 (舍去),
(舍去),
故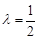 .
.
方法二:
(Ⅰ) 证明:延长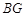 交
交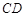 于
于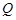 ,连
,连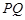 ,
,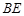 .得平行四边形
.得平行四边形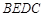 ,则
,则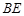 //
// 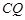 ,
,
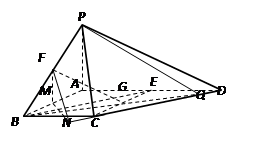
所以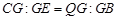 .
.
又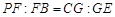 ,则
,则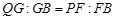 ,
,
所以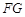 //
//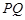 .
.
因为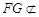 平面
平面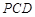 ,
,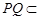 平面
平面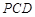 ,
,
所以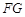 //平面
//平面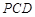 . …………6分
. …………6分
(Ⅱ)解:作FM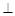
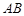 于
于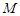 ,作
,作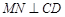 于
于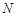 ,连
,连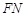 .
.
则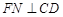 ,
,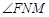 为二面角
为二面角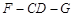 的平面角.
的平面角.
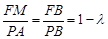 ,不妨设
,不妨设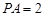 ,则
,则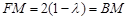 ,
,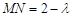 ,
,
由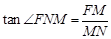 得
得 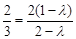 ,即
,即 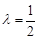 .
.
(Ⅰ) 证明:如图以点A为原点建立空间直角坐标系A-xyz,其中K为BC的中点,
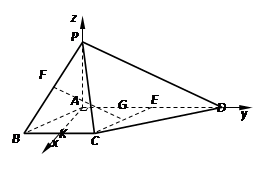
不妨设PA=2,则
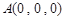 ,
,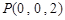 ,
,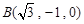 ,
,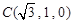 ,
,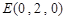 ,
,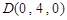 .
.由
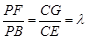 ,得
,得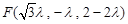 ,
,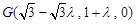 ,
,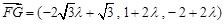 ,
,设平面
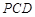 的法向量
的法向量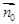 =(x,y,z),则
=(x,y,z),则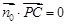 ,
,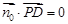 ,
,得
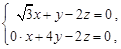
可取
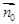 =(
=(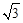 ,1,2),于是
,1,2),于是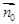
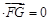 ,故
,故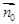
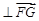 ,又因为FG
,又因为FG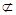 平面PDC,即
平面PDC,即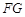 //平面
//平面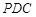 .
. (Ⅱ) 解:
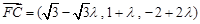 ,
,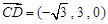 ,
,设平面
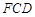 的法向量
的法向量 ,则
,则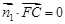 ,
,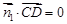 ,
,可取
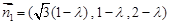 ,又
,又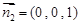 为平面
为平面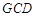 的法向量.
的法向量.由
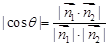 ,因为tan
,因为tan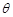 =
=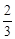 ,cos
,cos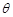 =
=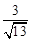 ,
,所以
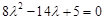 ,解得
,解得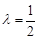 或
或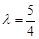 (舍去),
(舍去),故
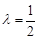 .
. 方法二:
(Ⅰ) 证明:延长
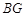 交
交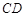 于
于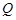 ,连
,连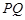 ,
,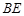 .得平行四边形
.得平行四边形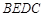 ,则
,则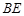 //
// 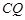 ,
,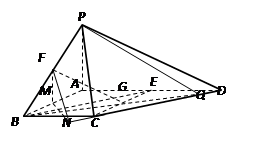
所以
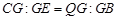 .
.又
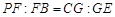 ,则
,则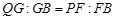 ,
,所以
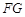 //
//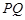 .
.因为
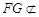 平面
平面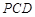 ,
,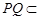 平面
平面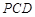 ,
,所以
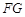 //平面
//平面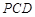 . …………6分
. …………6分(Ⅱ)解:作FM
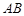 于
于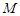 ,作
,作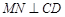 于
于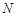 ,连
,连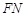 .
.则
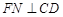 ,
,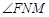 为二面角
为二面角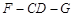 的平面角.
的平面角.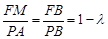 ,不妨设
,不妨设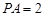 ,则
,则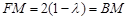 ,
,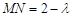 ,
,由
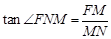 得
得 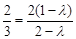 ,即
,即 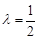 .
.略

练习册系列答案
相关题目
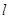 、
、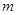 ,两个不重合的平面α、β,
,两个不重合的平面α、β,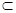 β,给出下列命题:①α∥β
β,给出下列命题:①α∥β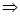
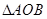 中,
中,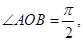 AB=2OB=4,D为AB的中点,若
AB=2OB=4,D为AB的中点,若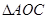 是
是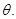 (I)若
(I)若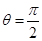 ,求证:平面
,求证:平面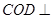 平面AOB;(II)若
平面AOB;(II)若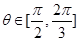 时,求二面角C—OD—B的余弦值的最小值。
时,求二面角C—OD—B的余弦值的最小值。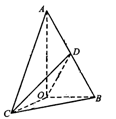
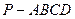 中,底面
中,底面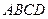 是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.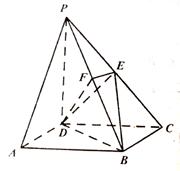

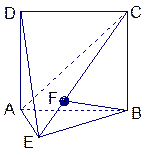
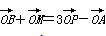 ,则点P与A、B、M( )
,则点P与A、B、M( )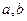 ,
,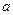 ∥平面
∥平面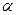 ,
,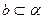 ,则直线
,则直线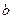 的位置关系是 .
的位置关系是 .