题目内容
(本题满分12分)如图,已知四棱锥P—ABCD中,底面ABCD为菱形,PA 平面ABCD,
平面ABCD, ,BC=1,E为CD的中点,PC与平面ABCD成
,BC=1,E为CD的中点,PC与平面ABCD成 角。
角。
(1)求证:平面EPB 平面PBA;(2)求二面角P-BD-A 的余弦值
平面PBA;(2)求二面角P-BD-A 的余弦值
证明:(1)连接BE
证得 ;由
;由
平面EPB 平面PBA;
平面PBA;
(2)cos =
= 。
。
解析试题分析:证明:(1)连接BE
因为EC= ,BC=1,
,BC=1,

又AB//CD

所以,平面EPB 平面PBA……………….6
平面PBA……………….6
(2)连AC,BD交于O 又
又
所以
 为二面角P-BD-A的平面角,----------8
为二面角P-BD-A的平面角,----------8 -------10
-------10 cos
cos =
= -------12
-------12
考点:本题主要考查立体几何的面面垂直,二面角的计算。
点评:本题通过考查平面与平面的垂直关系及二面角的计算,考查空间想像能力、推理论证能力、运算求解能力、考查化归与转化思想,函数与方程思想等.立体几何中的计算问题,要遵循“一作、二证、三计算”的步骤。属中档题。

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 中,
中, ,
, ,
, ,
, 为
为 上一点,
上一点,  ,且
,且 .将梯形
.将梯形 折成直二面角
折成直二面角 ,如图2所示.
,如图2所示.
 平面
平面 ;
; 关于点
关于点 的对称点为
的对称点为 ,点
,点 在
在 所在平面内,且直线
所在平面内,且直线 与平面
与平面 所成的角为
所成的角为 ,试求出点
,试求出点 的最短距离.
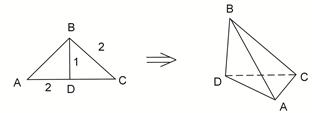
的最短距离. 中,
中, 为
为 边上的高,
边上的高, ,
, ,沿
,沿 翻折,使得
翻折,使得 ,得到几何体
,得到几何体 。
。
 ;
; 与平面
与平面 所成角的正切值。
所成角的正切值。 与三棱柱
与三棱柱 的组合体,其中,圆柱
的组合体,其中,圆柱 是边长为4的正方形,
是边长为4的正方形,
 为等腰直角三角形,
为等腰直角三角形, .
.
 中,底面
中,底面 是直角梯形,
是直角梯形, ∥
∥ ,∠
,∠ ,
,  ,平面
,平面 ⊥平面
⊥平面 .
.
 和平面
和平面 所成二面角(小于
所成二面角(小于 )的大小;
)的大小; 上是否存在点
上是否存在点 使得
使得 ∥平面
∥平面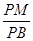 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 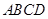 ⊥平面
⊥平面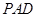 ,
, 是直角三角形,
是直角三角形,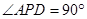 ,四边形
,四边形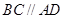 ,
,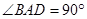 ,
, ,且
,且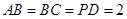 ,
,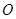 是
是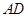 的中点,
的中点,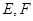 分别是
分别是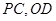 的中点.
的中点. 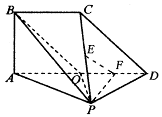
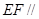 平面
平面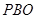 ;
;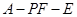 的正切值.
的正切值.
 的长; (2)求cos<
的长; (2)求cos< >的值; (3)求证:A1B⊥C1M.
>的值; (3)求证:A1B⊥C1M.  ,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE =
,AB=BC=2AD=4,E、F分别是AB、CD上的点,且EF∥BC。设AE = ,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
 ,求
,求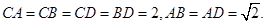

 平面BCD;
平面BCD;