题目内容
已知函数 ,且方程
,且方程 有两个实根为
有两个实根为 .
.
(1)求函数 的解析式 ;
的解析式 ;
(2)设 ,解关于x的不等式:
,解关于x的不等式: .
.
 ,且方程
,且方程 有两个实根为
有两个实根为 .
.(1)求函数
 的解析式 ;
的解析式 ; (2)设
 ,解关于x的不等式:
,解关于x的不等式: .
.(1) ;(2)(ⅰ)当
;(2)(ⅰ)当 当
当 (ⅲ)当
(ⅲ)当 .
.
 ;(2)(ⅰ)当
;(2)(ⅰ)当 当
当 (ⅲ)当
(ⅲ)当 .
.试题分析:(1)根据方程解的定义,把两角-2和1代入方程,就可得到关于
 的两个等式,把它们作为
的两个等式,把它们作为 的方程,联立方程组可解出
的方程,联立方程组可解出 ;(2)先把
;(2)先把 ,再转化为整式不等式
,再转化为整式不等式 ,一定要注意不等式左边各因式中最高次项系数均为正,实质上此时对应的方程的解也就出来了,但要写出不等式的解集,还必须讨论解的大小.
,一定要注意不等式左边各因式中最高次项系数均为正,实质上此时对应的方程的解也就出来了,但要写出不等式的解集,还必须讨论解的大小.试题解析:(1)将
 分别代入方程
分别代入方程
所以
 。 4分
。 4分(2)不等式即为
 ,
,即
 。 6分
。 6分(ⅰ)当
 8分
8分(ⅱ)当
 10分
10分(ⅲ)当
 。 12分
。 12分
练习册系列答案
相关题目
 ,(1)当a=2时,求关于x的不等式
,(1)当a=2时,求关于x的不等式 的解集;(2)当a>0时,求关于x的不等式
的解集;(2)当a>0时,求关于x的不等式 的解集.
的解集. ,不等式
,不等式 的解集为
的解集为 ,且
,且 ,则
,则 的取值范围是 ( )
的取值范围是 ( )

 或
或
 或
或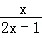 <0的解为 .
<0的解为 . 的解集为( )
的解集为( )



 的不等式
的不等式 .
. 时,解该不等式;
时,解该不等式; 时,解该不等式.
时,解该不等式. <
< 的解集是 ( )
的解集是 ( ) 的解集是________.
的解集是________.