题目内容
已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上取两个点，将其坐标记录于下表中：| C1 | C2 | |||
| x | 2 |  | 4 | 3 |
| y | 0 | 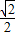 | 4 | -2 |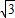
【答案】分析：根据椭圆、抛物线焦点的位置设出两个圆锥曲线的方程，将椭圆及抛物线上的点的坐标代入所设方程求出待定的系数即可．
解答：解：设椭圆的方程为
；抛物线方程y2=mx
将（2，0），（
）代入椭圆方程得a2=4，b2=1
将（4，4），（3，
）代入抛物线方程得到m=4
所以C1、C2的标准方程分别为：
；y2=4x
故答案为
；y2=4x
点评：求圆锥曲线的方程一般先判断出焦点的位置，在据方程形式设出方程，利用待定系数法求出方程．
解答：解：设椭圆的方程为
；抛物线方程y2=mx将（2，0），（
）代入椭圆方程得a2=4，b2=1将（4，4），（3，
）代入抛物线方程得到m=4所以C1、C2的标准方程分别为：
；y2=4x故答案为
；y2=4x点评：求圆锥曲线的方程一般先判断出焦点的位置，在据方程形式设出方程，利用待定系数法求出方程．
练习册系列答案
相关题目
已知椭圆C1、抛物线C2的焦点均在x轴上，C1的中心和C2的顶点均为原点O，从每条曲线上取两个点，将其坐标记录于下表中：
则C1、C2的标准方程分别为 、 ．
| C1 | C2 | |||||||||
| x | 2 |
|
4 | 3 | ||||||
| y | 0 |
|
4 | -2
| ||||||