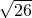题目内容
从点P（m，2）向圆（x+3）2+（y+3）2=1引切线，则切线长的最小值为（ ）A．
B．5
C．
D．3
【答案】分析：因为过P点的圆的切线长，圆半径，以及P点到圆心距离构成直角三角形，又因为圆半径为定植1，所以要求切线长的最小值，只需求P点到圆心距离的最小值即可．
解答：解：设圆心为C，切点为A，连接PC，PA，AC
∵PA为圆C的切线，∴PA⊥AC
∴PA2+AC2=PC2，
∴当PC最小时，PA有最小值．
∵P（m，2，C（-3，-3），∴PCmin=5，此时PA=
=
故选A
点评：本题主要考查了圆的切线与圆的位置关系的判断，属于圆方程的常规题．
解答：解：设圆心为C，切点为A，连接PC，PA，AC
∵PA为圆C的切线，∴PA⊥AC
∴PA2+AC2=PC2，
∴当PC最小时，PA有最小值．
∵P（m，2，C（-3，-3），∴PCmin=5，此时PA=
=故选A
点评：本题主要考查了圆的切线与圆的位置关系的判断，属于圆方程的常规题．
练习册系列答案
名师伴你成长课时同步学练测系列答案
相关题目
从点P（m，3）向圆C：（x+2）2+（y+2）2=1引切线，则切线长的最小值是（ ）
A、2
| ||
| B、5 | ||
C、
| ||
D、4+
|
