题目内容
(本小题满分12分)已知二次函数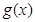 对任意实数
对任意实数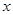 都满足
都满足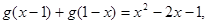 且
且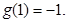
(Ⅰ)求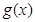 的表达式;
的表达式;
(Ⅱ)设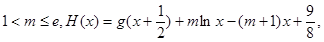 求证:
求证: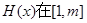 上为减函数;
上为减函数;
(Ⅲ)在(Ⅱ)的条件下,证明:对任意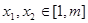 ,恒有
,恒有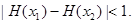
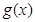 对任意实数
对任意实数 都满足
都满足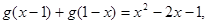 且
且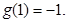
(Ⅰ)求
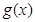 的表达式;
的表达式;(Ⅱ)设
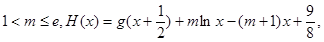 求证:
求证: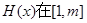 上为减函数;
上为减函数;(Ⅲ)在(Ⅱ)的条件下,证明:对任意
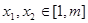 ,恒有
,恒有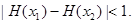
(Ⅰ)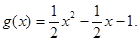 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析
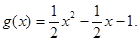 (Ⅱ)见解析(Ⅲ)见解析
(Ⅱ)见解析(Ⅲ)见解析试题分析:(1)设
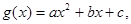
于是
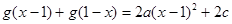
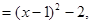
所以
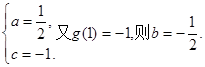
所以
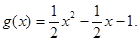 ………………5分
………………5分(2)
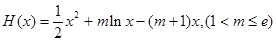 …………6分
…………6分因为对

故
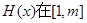 上为减函数 ………………8分
上为减函数 ………………8分(3)由(2)得:
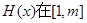 上为减函数则:
上为减函数则: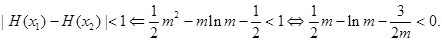 …………10分
…………10分记
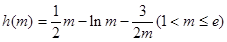 ,
,则
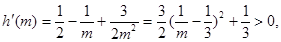 ………………11分
………………11分所以
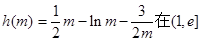 是单调增函数,
是单调增函数,所以
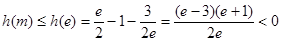 ,故命题成立 …………12分
,故命题成立 …………12分点评:(Ⅲ)中证明不等式恒成立转化为求函数最值问题,这是一种常用的转化思路

练习册系列答案
相关题目
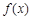 ,且
,且 ,则
,则 .
. 满足
满足 且
且 .
. 的解析式;
的解析式;  时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围. 有两个不同的零点,则
有两个不同的零点,则 的取值范围是( )
的取值范围是( )



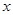 2+(2k-3)
2+(2k-3) 的部分图像如右图所示,则函数
的部分图像如右图所示,则函数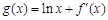 的零点所在的区间是( )
的零点所在的区间是( )
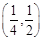



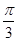 ﹞的最大值并求出相应的x值.
﹞的最大值并求出相应的x值.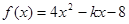 在区间(5,20)不是单调函数,那么实数k的取值范围是____________________________.
在区间(5,20)不是单调函数,那么实数k的取值范围是____________________________.