题目内容
设[x]是不超过x的最大整数,则[log31]+[log32]+[log33]+[log34]+…+[log3500]=
2142
2142
.分析:先根据对数的运算性质判断[log31]、[log32]、[log33]…[log3500]的大小,最后加起来即可.
解答:解:由题意可知:设[log3a]=b
log3a=b+x,a,b为整数
a=3b+x,0≤x<1,
因为y=3x为单调增函数
当a在[1,2]时
因为30=1,31=3
则0<b+x<1
所以b=0时,[log31]=[log32]=0
当a在[3,8]时
同理1<b+x<2
b=1时,[log33]=[log34]=…=[log38]=1
b=2时,[log39]=[log310]=…=[log326]=2.
b=3时,[log327]=[log328]=…=[log380]=3.
b=4时,[log381]=[log382]=…=[log3242]=4.
b=5时,[log3243]=[log3244]=[log3245]=…=[log3500]=5.
∴[log31]+[log32]+[log33]+[log34]+…+[log3500]
=0×(31-30)+1×(32-31)+2×(33-32)+3×(34-33)+4×(35-34)+5×(500-243+1)
=1×6+2×18+3×54+4×162+5×257
=1×6+2×18+3×54+4×162+5×257=2142.
故答案为:2142.
log3a=b+x,a,b为整数
a=3b+x,0≤x<1,
因为y=3x为单调增函数
当a在[1,2]时
因为30=1,31=3
则0<b+x<1
所以b=0时,[log31]=[log32]=0
当a在[3,8]时
同理1<b+x<2
b=1时,[log33]=[log34]=…=[log38]=1
b=2时,[log39]=[log310]=…=[log326]=2.
b=3时,[log327]=[log328]=…=[log380]=3.
b=4时,[log381]=[log382]=…=[log3242]=4.
b=5时,[log3243]=[log3244]=[log3245]=…=[log3500]=5.
∴[log31]+[log32]+[log33]+[log34]+…+[log3500]
=0×(31-30)+1×(32-31)+2×(33-32)+3×(34-33)+4×(35-34)+5×(500-243+1)
=1×6+2×18+3×54+4×162+5×257
=1×6+2×18+3×54+4×162+5×257=2142.
故答案为:2142.
点评:本题考查对数的运算法则,解题时要注意公式的灵活运用,同时要注意总结规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ]=1),对于给定的n∈N*,定义
]=1),对于给定的n∈N*,定义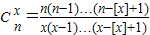 ,x∈[1,+∞),则当x∈
,x∈[1,+∞),则当x∈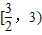 时,函数C8x的值域是( )
时,函数C8x的值域是( )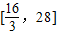
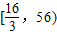
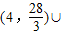 [28,56)
[28,56)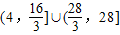
 ]=1),对于给定的n∈N*,定义
]=1),对于给定的n∈N*,定义 ,x∈[1,+∞),则当x∈
,x∈[1,+∞),则当x∈ 时,函数C8x的值域是( )
时,函数C8x的值域是( )

 [28,56)
[28,56)
 ]=1),对于给定的n∈N*,定义
]=1),对于给定的n∈N*,定义 ,x∈[1,+∞),则当x∈
,x∈[1,+∞),则当x∈ 时,函数C8x的值域是( )
时,函数C8x的值域是( )

 [28,56)
[28,56)
 ]=1),对于给定的n∈N*,定义
]=1),对于给定的n∈N*,定义 ,x∈[1,+∞),则当x∈
,x∈[1,+∞),则当x∈ 时,函数C8x的值域是( )
时,函数C8x的值域是( )

 [28,56)
[28,56)