题目内容
(2012•孝感模拟)已知数列{an}满足:a1+a2+a3+…+an=n-an,(n=1,2,3,…)
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+
t≤t2,求实数t的取值范围.
(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n=1,2,3,…),如果对任意n∈N*,都有bn+
| 1 | 4 |
分析:(Ⅰ)利用a1+a2+a3+…+an=n-an,再写一式,两式相减,整理可得数列{an-1是以-
为首项,以
为公比的等比数列;(Ⅱ)先确定bn=(2-n)(an-1)=
,再利用bn+1-bn,确定bn有最大值b3=b4=
,从而对任意n∈N*,都有bn+
t≤t2,等价于对任意n∈N*,都有
≤t2-
t成立,由此可求实数t的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
| n-2 |
| 2n |
| 1 |
| 8 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
解答:(Ⅰ)证明:由题可知:a1+a2+a3+…+an=n-an,①
a1+a2+a3+…+an+1=n+1-an+1,②
②-①可得2an+1-an=1 …..(3分)
即:an+1-1=
(an-1),又a1-1=-
…..(5分)
所以数列{an-1是以-
为首项,以
为公比的等比数列….…..(6分)
(Ⅱ)解:由(Ⅰ)可得an=1-(
)n,…(7分)
∴bn=(2-n)(an-1)=
…(8分)
由bn+1-bn=
-
=
>0可得n<3
由bn+1-bn<0可得n>3 …(9分)
所以b1<b2<b3=b4,b4>b5>…>bn>…
故bn有最大值b3=b4=
所以,对任意n∈N*,都有bn+
t≤t2,等价于对任意n∈N*,都有
≤t2-
t成立…(13分)
所以t2-
t-
≥0
解得t≥
或t≤-
所以,实数t的取值范围是(-∞,-
]∪[
,+∞) …(14分)
a1+a2+a3+…+an+1=n+1-an+1,②
②-①可得2an+1-an=1 …..(3分)
即:an+1-1=
| 1 |
| 2 |
| 1 |
| 2 |
所以数列{an-1是以-
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)解:由(Ⅰ)可得an=1-(
| 1 |
| 2 |
∴bn=(2-n)(an-1)=
| n-2 |
| 2n |
由bn+1-bn=
| n+1-2 |
| 2n+1 |
| n-2 |
| 2n |
| 3-n |
| 2n+1 |
由bn+1-bn<0可得n>3 …(9分)
所以b1<b2<b3=b4,b4>b5>…>bn>…
故bn有最大值b3=b4=
| 1 |
| 8 |
所以,对任意n∈N*,都有bn+
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 4 |
所以t2-
| 1 |
| 4 |
| 1 |
| 8 |
解得t≥
| 1 |
| 2 |
| 1 |
| 4 |
所以,实数t的取值范围是(-∞,-
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查数列递推式,考查等比数列的证明,考查恒成立问题,确定数列的通项,求出数列的最大值是解题的关键.

练习册系列答案
相关题目
 (2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )
(2012•孝感模拟)如图,在A、B间有四个焊接点,若焊接点脱落,而可能导致电路不通,如今发现A、B之间线路不通,则焊接点脱落的不同情况有( )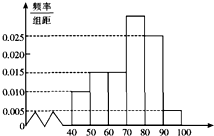 (2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题:
(2012•孝感模拟)某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如右图所示的部分频率分布直方图,请观察图形信息,回答下列问题: