题目内容
已知10个乒乓球中有2个次品.(1)任意取出4个乒乓球作检验,求其中恰有1个次品的概率.
(2)为了保证使2个次品全部检验出的概率不小于0.8,至少应抽取几个乒乓球?
解:(1)设10个乒乓球中取出4个,其中恰有1个次品的事件为A.则P(A)=![]() =
=![]() .因此,恰有一个次品的概率是
.因此,恰有一个次品的概率是![]() .
.
(2)设10个乒乓球中取出n个,其中有2个次品的事件为B.
则P(B)=![]() =
=![]() ·
·![]() =
=![]() ,
,
依题意,P(B)≥0.8,
即![]() ≥
≥![]() ,
,
亦即n2-n-72≥0.
又n∈N*,所以n≥9.
因此,至少抽取9个乒乓球才能满足题意.

 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案为了解某班学生喜爱打羽毛球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
|
|
|
50 |
已知在全部50人中随机抽取1人抽到不喜爱打羽毛球的学生的概率
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打羽毛球与性别有关?说明你的理由;
(3)已知喜爱打羽毛球的10位女生中, 还喜欢打篮球,
还喜欢打篮球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生
还喜欢踢足球,现在从喜欢打篮球、喜欢打乒乓球、喜欢踢足球的6位女生中各选出1名进行其他方面的调查,求女生 和
和 不全被选中的概率.下面的临界值表供参考:
不全被选中的概率.下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: 其中
其中 .)
.)
【解析】第一问利用数据写出列联表
第二问利用公式 计算的得到结论。
计算的得到结论。
第三问中,从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
 ,
,
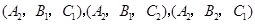 ,
,
基本事件的总数为8
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得
解:(1) 列联表补充如下:
|
|
喜爱打羽毛球 |
不喜爱打羽毛球 |
合计 |
|
男生 |
20 |
5 |
25 |
|
女生 |
10 |
15 |
25 |
|
合计 |
30 |
20 |
50 |
(2)∵
∴有99.5%的把握认为喜爱打篮球与性别有关
(3)从6位女生中选出喜欢打篮球、喜欢打乒乓球、喜欢踢足球的各1名,其一切可能的结果组成的基本事件如下:
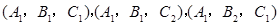 ,
,
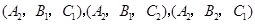 ,
,
基本事件的总数为8,
用 表示“
表示“ 不全被选中”这一事件,则其对立事件
不全被选中”这一事件,则其对立事件 表示“
表示“ 全被选中”这一事件,由于
全被选中”这一事件,由于 由
由 2个基本事件由对立事件的概率公式得
2个基本事件由对立事件的概率公式得 .
.

