题目内容
已知点M(3,5),在直线l:x-2y+2=0和y轴上各找一点P和Q,使△MPQ的周长最小.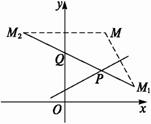 
解析：如题图,作点M关于直线l的对称点M1,再作点M关于y轴的对称点M2,连结M
由点M(3,5)及直线l,可求得点M关于直线l的对称点M1(5,1),同样容易求得点M关于y轴的对称点M2(-3,5).?
据M1和M2两点可得直线M
令x=0,得直线M
).?
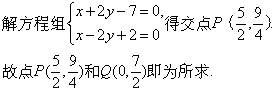
练习册系列答案
相关题目
已知点M(-3，0)，N(3，0)，设P(x，y)是曲线
+
=1上的点，则下列式子恒成立的是（ ）
| |x| |
| 5 |
| |y| |
| 4 |
| A、|PM|+|PN|=10 |
| B、|PM|-|PN|=10 |
| C、|PM|+|PN|≥10 |
| D、|PM|+|PN|≤10 |
已知点M（5，-6）和向量
=(1，-2)，若
=-3
，则点N的坐标为（ ）
| a |
| MN |
| a |
| A、（2，0） |
| B、（-3，6） |
| C、（6，2） |
| D、（-2，0） |
＝
，求点P的坐标．
,
) C.(-1,-1) D.(
,
)