题目内容
已知Rt△ABC的斜边两端点分别是B(4,0),C(-2,0),则顶点A的轨迹方程是
(x-1)2+y2=9(y≠0)
(x-1)2+y2=9(y≠0)
.分析:由于顶点A为Rt△ABC直角顶点,∴
•
=0,用坐标表示向量,进而可得轨迹方程,由于A,B,C构成直角三角形,属于要除去y=0的两点.
| AB |
| AC |
解答:解:设顶点A的坐标为(x,y)
∵A为直角顶点,∴
•
=0,
∴(4-x,-y)•(-2-x,-y)=0
即:(x-1)2+y2=9
∵A,B,C构成直角三角形
∴除去y=0的两点.
∴方程为:(x-1)2+y2=9(y≠0)
故答案为(x-1)2+y2=9(y≠0)
∵A为直角顶点,∴
| AB |
| AC |
∴(4-x,-y)•(-2-x,-y)=0
即:(x-1)2+y2=9
∵A,B,C构成直角三角形
∴除去y=0的两点.
∴方程为:(x-1)2+y2=9(y≠0)
故答案为(x-1)2+y2=9(y≠0)
点评:本题的考点是轨迹方程,主要考查向量与解析几何的结合,关键是利用向量的数量积得出方程,必须注意把不符合条件的点舍去.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
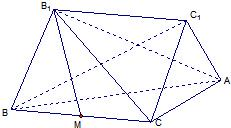 如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°
如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°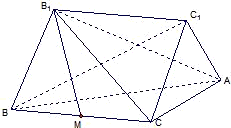 如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°
如图:已知BB1,CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1∥CC1,线段BB1的端点B1在平面ABC的射影M恰是BC的中点,已知BC=2,∠ACB=90°