题目内容
(文) {an}中,a1=1,an+1=
an+1,b1=1,(bn,bn+1)在直线x-y+2=0上.求:an,bn.
| 1 | 2 |
分析:①对于数列{an}中,由an+1=
an+1,变形为an+1-2=
(an-2),即可利用等比数列的通项公式求出;
②由于数列{bn}满足b1=1,(bn,bn+1)在直线x-y+2=0上,可得到bn-bn+1+2=0,变形利用等差数列的通项公式即可得出.
| 1 |
| 2 |
| 1 |
| 2 |
②由于数列{bn}满足b1=1,(bn,bn+1)在直线x-y+2=0上,可得到bn-bn+1+2=0,变形利用等差数列的通项公式即可得出.
解答:解:①∵{an}中,a1=1,an+1=
an+1,∴an+1-2=
(an-2),而a1-2=-1≠0,
∴数列 {an-2}是以-1为首项,
为公比的等比数列,
∴an-2=-(
)n-1,∴an=2-(
)n-1.
②∵数列{bn}满足b1=1,(bn,bn+1)在直线x-y+2=0上,
∴bn-bn+1+2=0,
∴bn+1-bn=2.
∴数列{bn}是以1为首项,2为公差的等差数列.
∴bn=1+2(n-1)=2n-1.
| 1 |
| 2 |
| 1 |
| 2 |
∴数列 {an-2}是以-1为首项,
| 1 |
| 2 |
∴an-2=-(
| 1 |
| 2 |
| 1 |
| 2 |
②∵数列{bn}满足b1=1,(bn,bn+1)在直线x-y+2=0上,
∴bn-bn+1+2=0,
∴bn+1-bn=2.
∴数列{bn}是以1为首项,2为公差的等差数列.
∴bn=1+2(n-1)=2n-1.
点评:熟练掌握等比数列、等差数列的定义及通项公式是解题的关键.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
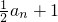 ,b1=1,(bn,bn+1)在直线x-y+2=0上.求:an,bn.
,b1=1,(bn,bn+1)在直线x-y+2=0上.求:an,bn. ,b1=1,(bn,bn+1)在直线x-y+2=0上.求:an,bn.
,b1=1,(bn,bn+1)在直线x-y+2=0上.求:an,bn.