题目内容
(2012•福州模拟)如图①,一条宽为l km的两平行河岸有村庄A和供电站C,村庄B与A、C的直线距离都是2km,BC与河岸垂直,垂足为D.现要修建电缆,从供电站C向村庄A、B供电.修建地下电缆、水下电缆的费用分别是2万元/km、4万元/km
(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.

(Ⅰ)已知村庄A与B原来铺设有旧电缆仰,需要改造,旧电缆的改造费用是0.5万元/km.现决定利用旧电缆修建供电线路,并要求水下电缆长度最短,试求该方案总施工费用的最小值.
(Ⅱ)如图②,点E在线段AD上,且铺设电缆的线路为CE、EA、EB.若∠DCE=θ (0≤θ≤
| P | 3 |
分析:(Ⅰ)由已知可得△ABC为等边三角形.因为CD⊥AD,所以水下电缆的最短线路为CD.过D作DE⊥AB于E,可知地下电缆的最短线路为DE、AB.由此能求出该方案的总费用.
(Ⅱ)因为∠DCE=θ,0≤θ≤
,所以CE=EB=
,ED=tanθ,AE=
-tanθ.(7分)则y=2×
+2
,令g(θ)=
,则g′(θ)=
,由此能求出施工总费用的最小值.
(Ⅱ)因为∠DCE=θ,0≤θ≤
| π |
| 3 |
| 1 |
| cosθ |
| 3 |
| 3-sinθ |
| cosθ |
| 3 |
| 3-sinθ |
| cosθ |
| 3sinθ-1 |
| cos2θ |
解答:(本小题满分13分)
解:(Ⅰ)由已知可得△ABC为等边三角形.
因为CD⊥AD,所以水下电缆的最短线路为CD.
过D作DE⊥AB于E,可知地下电缆的最短线路为DE、AB.(3分)
又CD=1,DE=
,AB=2,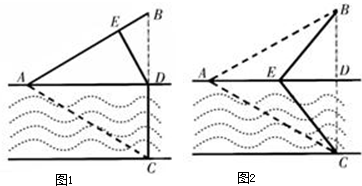
故该方案的总费用为
1×4+
×2+2×0.5=5+
.(万元) …(6分)
(Ⅱ)因为∠DCE=θ,0≤θ≤
,
所以CE=EB=
,ED=tanθ,AE=
-tanθ.(7分)
则y=
×4+
×2+(
-tanθ)×2
=2×
+2
,(9分)
令g(θ)=
,
则g′(θ)=
=
,(10分)
因为0≤θ≤
,所以0≤sinθ≤
,
记sinθ1=
,θ1∈(0,
),
当0≤sinθ<
,即0≤θ<θ1时,g′(θ)<0,
当
<sinθ≤
,即θ1<θ≤
时,g′(x)>0,
所以g(θ)min=g(θ1)=
=2
,
从而y≥4
+2
,(12分)
此时ED=tanθ1=
,
因此施工总费用的最小值为(4
+2
)万元,其中ED=
.(13分)
解:(Ⅰ)由已知可得△ABC为等边三角形.
因为CD⊥AD,所以水下电缆的最短线路为CD.
过D作DE⊥AB于E,可知地下电缆的最短线路为DE、AB.(3分)
又CD=1,DE=
| ||
| 2 |

故该方案的总费用为
1×4+
| ||
| 2 |
| 3 |
(Ⅱ)因为∠DCE=θ,0≤θ≤
| π |
| 3 |
所以CE=EB=
| 1 |
| cosθ |
| 3 |
则y=
| 1 |
| cosθ |
| 1 |
| cosθ |
| 3 |
=2×
| 3-sinθ |
| cosθ |
| 3 |
令g(θ)=
| 3-sinθ |
| cosθ |
则g′(θ)=
| -cos2θ-(3-sinθ)(-sinθ) |
| cos2θ |
=
| 3sinθ-1 |
| cos2θ |
因为0≤θ≤
| π |
| 3 |
| ||
| 2 |
记sinθ1=
| 1 |
| 3 |
| π |
| 3 |
当0≤sinθ<
| 1 |
| 3 |
当
| 1 |
| 3 |
| ||
| 2 |
| π |
| 3 |
所以g(θ)min=g(θ1)=
3-
| ||||
|
| 2 |
从而y≥4
| 2 |
| 3 |
此时ED=tanθ1=
| ||
| 4 |
因此施工总费用的最小值为(4
| 2 |
| 3 |
| ||
| 4 |
点评:本题考查函数在生产实际中的应用,综合性强,难度大.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
