题目内容
函数y=tanx（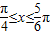
）的值域为 ．
【答案】分析：利用正切函数的图象与性质即可求得答案．
解答：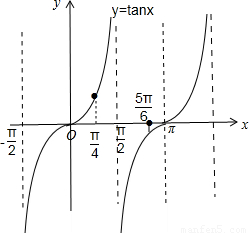
解：作出y=tanx的图象，
由图知，y=tanx在[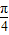
，
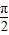）上单调递增，y≥1；
y=tanx在（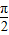
，
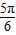]上单调递增，tan
=-
，
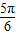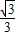∴此时，y≤-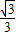
．
∴y=tanx（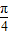
≤x≤
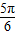）的值域为（-∞，-
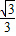]∪[1，+∞）．
故答案为：（-∞，-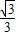
]∪[1，+∞）．
点评：本题考查正切函数的图象与性质，考查作图能力与运算能力，属于中档题．
解答：
解：作出y=tanx的图象，由图知，y=tanx在[
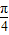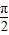，）上单调递增，y≥1；y=tanx在（
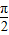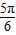，]上单调递增，tan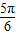=-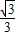，∴此时，y≤-
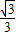．∴y=tan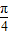x（
≤x≤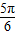）的值域为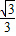（-∞，-]∪[1，+∞）．故答案为：（-∞，-
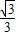]∪[1，+∞）．点评：本题考查正切函数的图象与性质，考查作图能力与运算能力，属于中档题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目