题目内容
如图，在圆C中，弦AB的长为2，则| AB |
| AC |
分析：过点C作CD⊥AB于D，可得AD=
AB=1，Rt△ACD中利用三角函数的定义算出cosA=
，再由向量数量积的公式加以计算，可得
•
的值．
| 1 |
| 2 |
| 1 | ||
|
| AB |
| AC |
解答：解：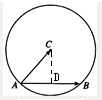
过点C作CD⊥AB于D，则D为AB的中点．
Rt△ACD中，AD=
AB=1，
可得cosA=
=
∴
•
=
•
cosA=
•
•
=
=2．
故答案为：2
过点C作CD⊥AB于D，则D为AB的中点．Rt△ACD中，AD=
| 1 |
| 2 |
可得cosA=
| AD |
| AC |
| 1 | ||
|
∴
| AB |
| AC |
| |AB| |
| |AC| |
| |AB| |
| |AC| |
| 1 | ||
|
| |AB| |
故答案为：2
点评：本题已知圆的弦长，求向量的数量积．着重考查了圆的性质、直角三角形中三角函数的定义与向量的数量积公式等知识，属于基础题．
练习册系列答案
相关题目
（2012•陕西）（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
，弦
，则
·
的值是
·
的值是
·
的值（ ）
·
的值是