题目内容
已知点P是抛物线y2=4x上的点,设点P到抛物线的准线的距离为d1,到圆(x+3)2+(y-3)2=1上一动点Q的距离为d2,则d1+d2的最小值是( )A.3
B.4
C.5
D.

【答案】分析:连接抛物线的焦点与圆心,由抛物线的定义知这两点连线的长度减去圆的半径即我所求的最小距离,根据两点之间的距离公式做出结果.
解答:解:连接抛物线的焦点与圆心,
由抛物线的定义知这两点连线的长度减去圆的半径即我所求的最小距离,
∵抛物线的焦点是(1,0)
圆心是(-3,3)
∴d1+d2的最小值是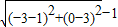 =4
=4
故选B.
点评:本题考查两点之间的距离公式和抛物线的简单性质,本题解题的关键是利用抛物线的定义把点到准线的距离转化成点到焦点的距离.
解答:解:连接抛物线的焦点与圆心,
由抛物线的定义知这两点连线的长度减去圆的半径即我所求的最小距离,
∵抛物线的焦点是(1,0)
圆心是(-3,3)
∴d1+d2的最小值是
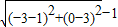 =4
=4故选B.
点评:本题考查两点之间的距离公式和抛物线的简单性质,本题解题的关键是利用抛物线的定义把点到准线的距离转化成点到焦点的距离.

练习册系列答案
相关题目
已知点P是抛物线y2=2x上的动点,点P在y轴上的射影是M,点A(
,4),则|PA|+|PM|的最小值是( )
| 7 |
| 2 |
| A、5 | ||
B、
| ||
| C、4 | ||
| D、AD |