题目内容
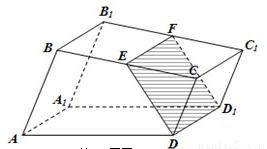
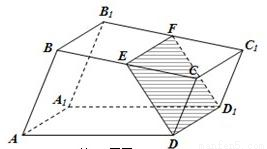
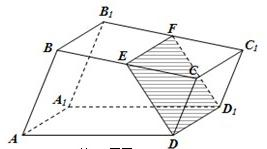
如图,已知直四棱柱ABCD﹣A1B1C1D1,底面ABCD为菱形,∠DAB=120°,E为线段CC1的中点,F为线段BD1的中点.
(Ⅰ)求证:EF∥平面ABCD;
(Ⅱ)当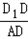 的比值为多少时,DF⊥平面D1EB,并说明理由.
的比值为多少时,DF⊥平面D1EB,并说明理由.
(Ⅰ)求证:EF∥平面ABCD;
(Ⅱ)当
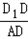 的比值为多少时,DF⊥平面D1EB,并说明理由.
的比值为多少时,DF⊥平面D1EB,并说明理由.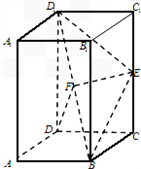
(Ⅰ)证明:连接AC1,由题意可知点F为AC1的中点.
∵因为点E为CC1的中点,
∴在△ACC1中,EF∥AC.
又∵EF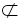 面ABCD,AC
面ABCD,AC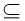 面ABCD,
面ABCD,
∴EF∥面ABCD.
(Ⅱ)解:当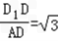 时,DF⊥平面D1EB.
时,DF⊥平面D1EB.
∵四边形ABCD为菱形,且∠DAB=120°,
∴
∵四棱柱ABCD﹣A1B1C1D1为直四棱柱,
∴四边形DBB1D1为矩形.
又 ,∴BD=DD1,
,∴BD=DD1,
∴四边形DBB1D1为正方形,
∴DF⊥D1B
在直四棱柱ABCD﹣A1B1C1D1中,DD1⊥底面ABCD,AC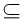 面ABCD,
面ABCD,
∴AC⊥DD1
∵四边形ABCD为菱形,AC⊥BD,BD∩DD1=D,
∴AC⊥面DBB1D1.
∵DF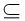 面DBB1D1,
面DBB1D1,
∴AC⊥DF,
又EF∥AC,
∴EF⊥DF.
∵EF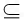 面D1EB,D1B
面D1EB,D1B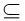 面D1EB,EF∩D1B=F,
面D1EB,EF∩D1B=F,
∴DF⊥平面D1EB.

∵因为点E为CC1的中点,
∴在△ACC1中,EF∥AC.
又∵EF
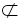 面ABCD,AC
面ABCD,AC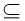 面ABCD,
面ABCD,∴EF∥面ABCD.
(Ⅱ)解:当
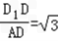 时,DF⊥平面D1EB.
时,DF⊥平面D1EB. ∵四边形ABCD为菱形,且∠DAB=120°,
∴

∵四棱柱ABCD﹣A1B1C1D1为直四棱柱,
∴四边形DBB1D1为矩形.
又
 ,∴BD=DD1,
,∴BD=DD1,∴四边形DBB1D1为正方形,
∴DF⊥D1B
在直四棱柱ABCD﹣A1B1C1D1中,DD1⊥底面ABCD,AC
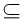 面ABCD,
面ABCD,∴AC⊥DD1
∵四边形ABCD为菱形,AC⊥BD,BD∩DD1=D,
∴AC⊥面DBB1D1.
∵DF
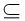 面DBB1D1,
面DBB1D1,∴AC⊥DF,
又EF∥AC,
∴EF⊥DF.
∵EF
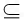 面D1EB,D1B
面D1EB,D1B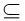 面D1EB,EF∩D1B=F,
面D1EB,EF∩D1B=F,∴DF⊥平面D1EB.


练习册系列答案
相关题目
 如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.
如图,已知直四棱柱ABCD-A1B1C1D1的底面是直角梯形,AB⊥BC,AB∥CD,E,F分别是棱BC,B1C1上的动点,且EF∥CC1,CD=DD1=1,AB=2,BC=3.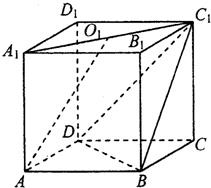 如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点.
如图,已知直四棱柱ABCD-A1B1C1D1的底面边长和侧棱长均为1,且满足∠BAD=60°,O1为A1C1的中点. 如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求:
如图,已知直四棱柱ABCD-A1B1C1D1的底面是边长为4的菱形,∠BAD=60°,AA1=6,P是棱AA1的中点.求: