题目内容
如图,正三棱柱 中,
中, ,
, 是侧棱
是侧棱 的中点.
的中点.

(Ⅰ)证明: ;
;
(Ⅱ)求二面角 的大小.
的大小.
 中,
中, ,
, 是侧棱
是侧棱 的中点.
的中点.
(Ⅰ)证明:
 ;
;(Ⅱ)求二面角
 的大小.
的大小.解:方法一:
(Ⅰ)证明:设 是
是 的中点,连接
的中点,连接 、
、 .
.
在正三棱柱中, ,
, 平面
平面 ,
,
∴ 是
是 在面
在面 上的射影.
上的射影.
易知 ≌
≌ ,
, .
.
又 ,
,
∴
 ,
, ,
,
∴ . ………………………………………6分
. ………………………………………6分
(Ⅱ)由(Ⅰ)知 平面
平面 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 ,
,

则 为二面角
为二面角 的平面角.
的平面角.
不妨设 ,则
,则 ,
, ,
,
在 中,
中, ,
,
∴ . ………………12分
. ………………12分
方法二:
(Ⅰ)在正三棱柱中,以 的中点
的中点 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 如图.
如图.
不妨设 ,则
,则
 ,
, ,
, ,
, ,
,
∴ ,
, ,
,
∵ .
.
∴ .………………………6分
.………………………6分
(Ⅱ)在空间直角坐标系 中,
中,

易知平面 的一个法向量为
的一个法向量为 .
.
设平面 的法向量为
的法向量为 ,
,
易知 ,
, .
.
由 得
得 ,取
,取 得
得 .
.
 ,
,
∴二面角 的的大小为
的的大小为 .………………………………………12分
.………………………………………12分
(Ⅰ)证明:设
 是
是 的中点,连接
的中点,连接 、
、 .
.在正三棱柱中,
 ,
, 平面
平面 ,
,∴
 是
是 在面
在面 上的射影.
上的射影.易知
 ≌
≌ ,
, .
.又
 ,
,∴

 ,
, ,
,∴
 . ………………………………………6分
. ………………………………………6分(Ⅱ)由(Ⅰ)知
 平面
平面 ,作
,作 ,垂足为
,垂足为 ,连结
,连结 ,
,
则
 为二面角
为二面角 的平面角.
的平面角.不妨设
 ,则
,则 ,
, ,
,在
 中,
中, ,
,∴
 . ………………12分
. ………………12分方法二:
(Ⅰ)在正三棱柱中,以
 的中点
的中点 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系 如图.
如图.不妨设
 ,则
,则 ,
, ,
, ,
, ,
,∴
 ,
, ,
,∵
 .
.∴
 .………………………6分
.………………………6分(Ⅱ)在空间直角坐标系
 中,
中,
易知平面
 的一个法向量为
的一个法向量为 .
.设平面
 的法向量为
的法向量为 ,
,易知
 ,
, .
.由
 得
得 ,取
,取 得
得 .
. ,
,∴二面角
 的的大小为
的的大小为 .………………………………………12分
.………………………………………12分略

练习册系列答案
相关题目

 的正方体
的正方体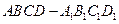 中,
中,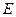 是线段
是线段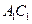 的中点,
的中点,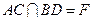 .
.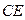 ^
^ ;
;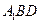 ;
;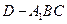 的体积.
的体积. 四面体
四面体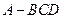 中,共顶点
中,共顶点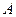 的三条棱两两互相垂直,且
的三条棱两两互相垂直,且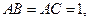 ,
,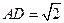 若四
若四 面体的四个顶点在一个球面上,则B,D的球面距离为_ ___ __。
面体的四个顶点在一个球面上,则B,D的球面距离为_ ___ __。 
 点,那么这两个切点在球面上的最短距离是 。
点,那么这两个切点在球面上的最短距离是 。