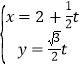题目内容
【题目】用数学归纳法证明:
(1)![]() ;
;
(2)![]() ;
;
(3)设![]() ,证明:
,证明: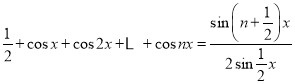 ;
;
(4)![]() 是13的倍数
是13的倍数![]() ;
;
(5)![]() ,证明
,证明![]() 能被
能被![]() 整除.
整除.
【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析;(4)证明见解析;(5)证明见解析;
【解析】
根据数学归纳法的方法步骤证明即可.
证明:(1)①当![]() 时,左边=右边=1;原等式成立
时,左边=右边=1;原等式成立
②假设当![]() 时,等式成立,即
时,等式成立,即![]() ,
,
当![]() 时,有
时,有
![]()
![]()
![]()
![]()
![]() .
.
所以,当![]() 时,等式成立.
时,等式成立.
由①②可知,对任意正整数![]() 都成立.
都成立.
(2)①当![]() 时,左边=右边=1,原等式成立;
时,左边=右边=1,原等式成立;
②假设当![]() 时,等式成立,
时,等式成立,
即![]() ,
,
当![]() 时,有
时,有
![]()
![]()
![]()
![]()
![]() .
.
所以,当![]() 时,等式也成立.
时,等式也成立.
由①②可知,对任意的正整数,
有![]() 都成立.
都成立.
(3)①当![]() 时,左边
时,左边![]() ,
,
右边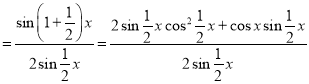
![]()
左边=右边,所以等式成立.
②假设当![]() 时,等式成立,
时,等式成立,
即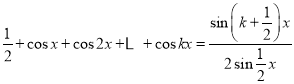 .
.
当![]() 时,有
时,有
![]()
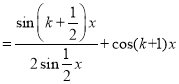
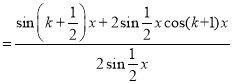
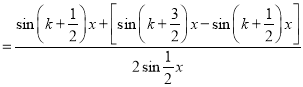
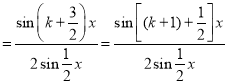 .
.
所以,当![]() 等式成立.
等式成立.
由①②可知,对任意的正整数,
有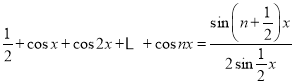 成立.
成立.
(4)①当![]() 时,
时,![]() ,
,
被13整除,所以结论成立.
②假设当![]() 时,结论成立,即
时,结论成立,即![]() 是13的倍数,
是13的倍数,
当![]() 时,
时,
![]()
![]()
![]()
![]() .
.
所以当![]() 时,
时,![]() 是13的倍数,结论成立.
是13的倍数,结论成立.
由①②可知,![]() 是13的倍数
是13的倍数![]() .
.
(5)①当![]() 时,
时,
原式![]()
![]()
![]()
所以,当![]() 时
时![]() 能被
能被![]() 整除.
整除.
②假设当![]() 时,结论成立,即
时,结论成立,即![]() 能被
能被![]() 整除.
整除.
当![]() 时,
时,
![]()
![]()
![]()
所以,当![]() 时,
时,![]() 能被
能被![]() 整除.
整除.
由①②可知,![]() 能被
能被![]() 整除.
整除.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目