题目内容
数列{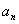 }的前n项和为
}的前n项和为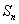 ,
,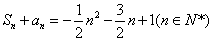 .
.
(Ⅰ)设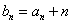 ,证明:数列
,证明:数列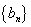 是等比数列;
是等比数列;
(Ⅱ)求数列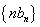 的前
的前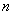 项和
项和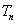 ;
;
(Ⅲ)若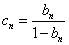 ,数列
,数列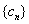 的前
的前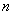 项和
项和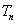 ,证明:
,证明: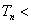
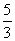 .
.
【解析】(I)因为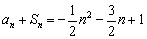 ,
,
所以 ① 当 时,
时,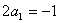 ,则
,则 ,
,
② 当 时,
时,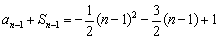 ,
,
所以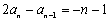 ,即
,即 ,
,
所以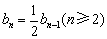 ,而
,而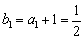 ,
,
所以数列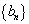 是首项为
是首项为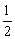 ,公比为
,公比为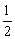 的等比数列,所以
的等比数列,所以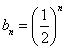 .
.
(II)由(1)得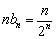 .
.
所以 ①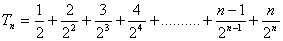 ,
,
②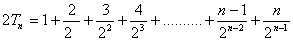 ,
,
②-①得: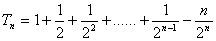 ,
,
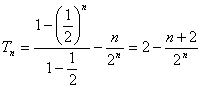
(III)由(I)知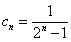
(1)当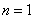 时,
时,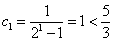 成立;
成立;
(2)当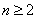 时,
时,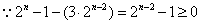 ,
,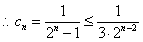 ,
,
所以 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
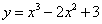 的单调递减区间是 .
的单调递减区间是 .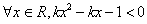 ”是真命题,则
”是真命题,则 的取值范围是 .
的取值范围是 . 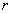 越小,说明两变量间的线性相关程度越低;
越小,说明两变量间的线性相关程度越低;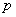 :“
:“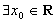 ,
,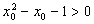 ”的否定
”的否定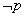 :“
:“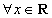 ,
,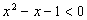 ”;
”;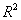 来刻画回归效果,若
来刻画回归效果,若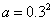 ,
,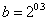 ,
,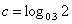 ,则
,则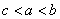 .
.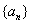 为等差数列,若
为等差数列,若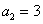 ,
,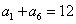 ,
,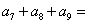 .
. 为等差数列,若
为等差数列,若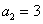 ,
,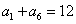 ,则
,则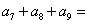
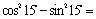 .
.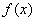 的定义域为开区间
的定义域为开区间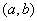 ,导函数
,导函数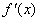 在
在
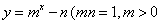 且
且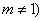 的大致图象为
的大致图象为