题目内容

已知函数f(x)=lg(mx2-mx+3).

(1)若f(x)定义域为R，求m的取值范围;

(2)若f(x)值域为R，求m的取值范围.

思路解析：令t=mx2-mx+3，(1)中f(x)定义域为R，意味着对任意实数x，t＞0恒成立，(2)中f(x)值域为R，意味着t可以取到(0，+∞)内的任一值.

解：(1)若f(x)定义域为R，

则mx2-mx+3＞0恒成立.

当m=0时，3＞0恒成立.

当m≠0时，则

解得0＜m＜12.综上可得m的取值范围是［0，12).

(2)若f(x)值域为R，则有mx2-mx+3可以取到(0，+∞)内的任一值.

所以

解得m≥12，

所以m的取值范围是［12，+∞).

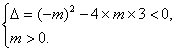
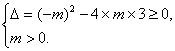
练习册系列答案
相关题目
已知函数f(x)=
1
3
x3-
3
2
ax2-(a-3)x+b
（1）若函数f（x）在P（0，f（0））的切线方程为y=5x+1，求实数a，b的值：
（2）当a＜3时，令g(x)=
f′(x)
x
，求y=g（x）在[l，2]上的最大值．
已知函数f(x)=
1
2
x2-alnx的图象在点P（2，f（2））处的切线方程为l：y=x+b
（1）求出函数y=f（x）的表达式和切线l的方程；
（2）当x∈[
1
e
，e]时（其中e=2.71828…），不等式f（x）＜k恒成立，求实数k的取值范围．
已知函数f(x)=lnx，g(x)=
12
x2+a（a为常数），直线l与函数f（x）、g（x）的图象都相切，且l与函数f（x）的图象的切点的横坐标为1．
（1）求直线l的方程及a的值；
（2）当k＞0时，试讨论方程f（1+x2）-g（x）=k的解的个数．
已知函数f(x)=
13
x3+x2+ax．
（1）讨论f（x）的单调性；
（2）设f（x）有两个极值点x1，x2，若过两点（x1，f（x1）），（x2，f（x2））的直线l与x轴的交点在曲线y=f（x）上，求a的值．
已知函数f(x)=x3-
32
ax2+b，a，b为实数，x∈R，a∈R．
（1）当1＜a＜2时，若f（x）在区间[-1，1]上的最小值、最大值分别为-2、1，求a、b的值；
（2）在（1）的条件下，求经过点P（2，1）且与曲线f（x）相切的直线l的方程；
（3）试讨论函数F（x）=（f′（x）-2x2+4ax+a+1）•ex的极值点的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网