题目内容
(本题满分12分)定义在R上的奇函数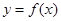 为减函数,
为减函数, 对
对 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
实数m的取值范围为 .
.
解析试题分析:根据题意可知函数是奇函数 ,同时又是定义域上的减函数,
,同时又是定义域上的减函数, ,要是不等式恒成立,则
,要是不等式恒成立,则 成立即可,利用三角的有界性得到求解。
成立即可,利用三角的有界性得到求解。
解:
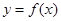 为奇函数,
为奇函数,

又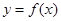 为减函数,
为减函数,

即
整理得: 恒成立,设
恒成立,设 下面只需求
下面只需求 的最大值,
的最大值,
而
可知


 实数m的取值范围为
实数m的取值范围为 .
.
考点:本题主要考查了三角函数的奇偶性和单调性的运用。
点评:解决该试题的关键是将已知表达式转化为 ,分离参数的思想来求解m的范围。
,分离参数的思想来求解m的范围。

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目

 ,求
,求 的表达式;
的表达式; 的图象关于原点对称,求函数
的图象关于原点对称,求函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. 的值.
的值. ,且
,且 ,
, ;
; ;
; 的值。
的值。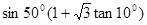 ,
,  ,求sin
,求sin 的值。
的值。 的图象与
的图象与 轴的交点为
轴的交点为 ,它在
,它在 和
和 .
. 的解析式及
的解析式及 的值;
的值; 满足
满足 ,求
,求 的值。
的值。 .
. 的最小正周期;
的最小正周期; 个单位得到函数g(x)的图象,求函数g(x)在区间
个单位得到函数g(x)的图象,求函数g(x)在区间 上的最大值和最小值。
上的最大值和最小值。 (
( )的图象过点
)的图象过点 .
. 的解析式;(Ⅱ)已知
的解析式;(Ⅱ)已知 ,
, ,求
,求 的值.
的值. ,
, ,函数
,函数 ,
, 的最小正周期;
的最小正周期; 时,求
时,求 的图像经过怎样的变换而得到。
的图像经过怎样的变换而得到。