��Ŀ����
��x��R�����庯��sgn��x��=
��1���� x2-3x+1=sgn��x�� �ĸ���
��2���躯��f��x��=[sgn��x-2��]•��x2-2|x|��f��x��=[sgn��x-2��]•x2-2
��������x�ķ���f��x��=x+a��3�������ʵ������ʵ��a��ȡֵ��Χ��
��3���ǵ㼯S={��x��y��|xsgn��x-1��•ysgn��y-1��=10��x��0��y��0} s={��x��y�����㼯T={��lgx��lgy��|��x��y����S}����㼯TΧ�ɵ�����������
|
��1���� x2-3x+1=sgn��x�� �ĸ���
��2���躯��f��x��=[sgn��x-2��]•��x2-2|x|��f��x��=[sgn��x-2��]•x2-2
|
��3���ǵ㼯S={��x��y��|xsgn��x-1��•ysgn��y-1��=10��x��0��y��0} s={��x��y�����㼯T={��lgx��lgy��|��x��y����S}����㼯TΧ�ɵ�����������
��������1�����ݷֶ��亯�������ʣ����÷�������˼���ܹ��Ƶ�����x2-3x+1=sgn��x���ĸ���
��2�����ں���f(x)=
����ԭ����ת��Ϊ��a=
���������ν��˼�����Ƶ�������x�ķ���f��x��=x+a��3�������ʵ����
��3�����P��x��y����T����10x��10y����S��������x•sgn��10x-1��+y•sgn��10y-1��=1���ɴ����÷�������˼��������㼯TΧ�ɵ�����������
��2�����ں���f(x)=
|
|
��3�����P��x��y����T����10x��10y����S��������x•sgn��10x-1��+y•sgn��10y-1��=1���ɴ����÷�������˼��������㼯TΧ�ɵ�����������
��� �⣺��1����x��0ʱ��sgn��x��=1��
�⣺��1����x��0ʱ��sgn��x��=1��
�ⷽ��x2-3x+1=1����x=3��x=0����������ȥ����
��x=0ʱ��sgn��x��=0��0���Ƿ���x2-3x+1=0�Ľ⣻
��x��0ʱ��sgn��x��=-1��
�ⷽ��x2-3x+1=-1����x=1��x=2��������������ȥ����
����������x=3�Ƿ���x2-3x+1=sgn��x���ĸ���
��2�����ں���f(x)=
��
��ԭ����ת��Ϊ��a=
��
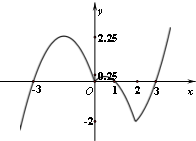
���ν�Ͽ�֪��
��a��-2ʱ��ԭ������1��ʵ����
�ڵ�a=-2ʱ��ԭ������2��ʵ����
�۵�-2��a��0ʱ��ԭ������3��ʵ����
�ܵ�a=0ʱ��ԭ������4��ʵ����
�ݵ�0��a��
ʱ��ԭ������5��ʵ����
��a=
ʱ��ԭ������4��ʵ����
�ߵ�
��a��
ʱ��ԭ������3��ʵ����
�൱a=
ʱ��ԭ������2��ʵ����
�ᵱa��
ʱ��ԭ������1��ʵ����
�ʵ�a��( -2 �� 0 )��(
��
)ʱ��
����x�ķ���f��x��=x+a��3�������ʵ����
��3�����P��x��y����T����10x��10y����S��
�����У�10x��sgn��10x-1��•��10y��sgn��10y-1��=10��
��x•sgn��10x-1��+y•sgn��10y-1��=1��
��x��0ʱ��10x-1��0��sgn����10x-1����xsgn��10x-1����
��x��0ʱ��10x-1��0��sgn��10x-1��=-1��xsgn��10x-1��=-1��
��x=0ʱ��xsgn��10x-1��=0=0��
��x•sgn��10x-1��=|x|��
ͬ����y•sgn��10y-1��=|y|��
��T={��x��y��||x|+|y|=1}��
�㼯TΧ�ɵ�������һ���߳�Ϊ
�������Σ����Ϊ2��
 �⣺��1����x��0ʱ��sgn��x��=1��
�⣺��1����x��0ʱ��sgn��x��=1���ⷽ��x2-3x+1=1����x=3��x=0����������ȥ����
��x=0ʱ��sgn��x��=0��0���Ƿ���x2-3x+1=0�Ľ⣻
��x��0ʱ��sgn��x��=-1��
�ⷽ��x2-3x+1=-1����x=1��x=2��������������ȥ����
����������x=3�Ƿ���x2-3x+1=sgn��x���ĸ���
��2�����ں���f(x)=
|
��ԭ����ת��Ϊ��a=
|
���ν�Ͽ�֪��
��a��-2ʱ��ԭ������1��ʵ����
�ڵ�a=-2ʱ��ԭ������2��ʵ����
�۵�-2��a��0ʱ��ԭ������3��ʵ����
�ܵ�a=0ʱ��ԭ������4��ʵ����
�ݵ�0��a��
| 1 |
| 4 |
��a=
| 1 |
| 4 |
�ߵ�
| 1 |
| 4 |
| 9 |
| 4 |
�൱a=
| 9 |
| 4 |
�ᵱa��
| 9 |
| 4 |
�ʵ�a��( -2 �� 0 )��(
| 1 |
| 4 |
| 9 |
| 4 |
����x�ķ���f��x��=x+a��3�������ʵ����
��3�����P��x��y����T����10x��10y����S��
�����У�10x��sgn��10x-1��•��10y��sgn��10y-1��=10��
��x•sgn��10x-1��+y•sgn��10y-1��=1��
��x��0ʱ��10x-1��0��sgn����10x-1����xsgn��10x-1����
��x��0ʱ��10x-1��0��sgn��10x-1��=-1��xsgn��10x-1��=-1��
��x=0ʱ��xsgn��10x-1��=0=0��
��x•sgn��10x-1��=|x|��
ͬ����y•sgn��10y-1��=|y|��
��T={��x��y��||x|+|y|=1}��
�㼯TΧ�ɵ�������һ���߳�Ϊ
| 2 |
���������⿼�鷽�̵ĸ�������������������ʵ����ȡֵ��Χ�����������������������ʱҪ�������⣬��ϸ���ע��ȼ�ת��˼��ĺ������ã�

��ϰ��ϵ�д�
 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�
�����Ŀ
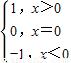
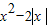 ��������x�ķ���f��x��=x+a��3�������ʵ������ʵ��a��ȡֵ��Χ��
��������x�ķ���f��x��=x+a��3�������ʵ������ʵ��a��ȡֵ��Χ��