题目内容
(2014•广东模拟)某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为
.
(Ⅰ)求选手甲可进入决赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望.
| 2 | 3 |
(Ⅰ)求选手甲可进入决赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望.
分析:(Ⅰ)由于答对3题者直接进入决赛,故可分为三类:一类是三题全对;一类是答4题,前3题错一题,第4题答对;一类是答5题,前4题错两题,第5题答对,故可求求选手甲可进入决赛的概率;
(Ⅱ)依题意,ξ的可能取值为3,4,5.利用独立重复试验的概率公式分别求出相应的概率,从而得出ξ的分布列,进而可求概率.
(Ⅱ)依题意,ξ的可能取值为3,4,5.利用独立重复试验的概率公式分别求出相应的概率,从而得出ξ的分布列,进而可求概率.
解答:解:(Ⅰ) 选手甲答3道题可进入决赛的概率为(
)3=
; …1分
选手甲答4道题可进入决赛的概率为
(
)2•
•
=
;…3分
选手甲答5道题可进入决赛的概率为
(
)2•(
)2•
=
; …5分
∴选手甲可进入决赛的概率p=
+
+
=
. …7分
(Ⅱ)依题意,ξ的可能取值为3,4,5.则有p(ξ=3)=(
)3+(
)3=
,p(ξ=4)=
(
)2•
•
+
(
)2•
•
=
,p(ξ=5)=
(
)2•(
)2•
+
(
)2•(
)2•
=
,…10分
因此,有
∴Eξ=3•
+4•
+5•
=
=3
. …12分.
| 2 |
| 3 |
| 8 |
| 27 |
选手甲答4道题可进入决赛的概率为
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 8 |
| 27 |
选手甲答5道题可进入决赛的概率为
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 16 |
| 81 |
∴选手甲可进入决赛的概率p=
| 8 |
| 27 |
| 8 |
| 27 |
| 16 |
| 81 |
| 64 |
| 81 |
(Ⅱ)依题意,ξ的可能取值为3,4,5.则有p(ξ=3)=(
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
因此,有
| ξ | 3 | 4 | 5 | ||||||
| p |
|
|
|
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |
| 26 |
| 27 |
点评:本题的考点是离散型随机变量的期望与方差,主要考查等可能事件的概率,考查离散型随机变量的分布列和期望,考查独立重复试验的概率公式,本题是一个综合题目,考查的知识点比较全面,在应用独立重复试验的概率公式时,注意数字运算不要出错.

练习册系列答案
相关题目
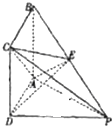 (2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.
(2014•广东模拟)如图,四棱锥P-ABCD的底面ABCD是正方形,PD⊥平面ABCD,E为PB上的点,且2BE=EP.