已知圆C:(x-2)2+2=1.当m变化时.圆C上的点与原点的最短距离是1．题目和参考答案——青夏教育精英家教网—

题目内容

8．已知圆C：（x-2）²+（y+m-4）²=1，当m变化时，圆C上的点与原点的最短距离是1．

分析求出圆的圆心和半径，再求出|OC|的最小值，用|OC|的最小值减去半径，即得所求．

解答解：圆C：（x-2）²+（y+m-4）²=1表示圆心为C（-2，-m+4），半径R=1的圆，
求得|OC|=$\sqrt{4+（-m+4）^{2}}$，
∴m=4时，|OC|的最小值为2
故当m变化时，圆C上的点与原点的最短距离是|OC|的最小值-R=2-1=1，
故答案为：1．

点评本题主要考查点和圆的位置关系，两点间的距离公式的应用，属于中档题．

练习册系列答案

19．给出下列六个命题：
（1）若f（x-1）=f（1-x），则函数f（x）的图象关于直线x=1对称．
（2）y=f（x-1）与y=f（1-x）的图象关于直线x=0对称．
（3）y=f（x+3）的反函数与y=f^-1（x+3）是相同的函数．
（4）$y={（{\frac{1}{2}}）^{|x|}}-{sin^2}$x+2015无最大值也无最小值．
（5）y=$\frac{2tanx}{{1-{{tan}^2}x}}$的周期为π．
（6）y=sinx（0≤x≤2π）有对称轴两条，对称中心三个．
则正确命题的个数是（　　）

16．在半径为1的圆周上随机选取三点，它们构成一个锐角三角形的概率是（　　）

3．已知不同直线a，b，l，不同平面α，β，γ，则下列命题正确的是（　　）

13．

如图，已知圆C的圆心在y轴的正半轴上，且与x轴相切，圆C与直线y=kx+3相交于A，B两点．当$k=\sqrt{3}$时，$|AB|=\sqrt{15}$．
（Ⅰ）求圆C的方程；
（Ⅱ）当k取任意实数时，问：在y轴上是否存在定点T，使得∠ATB始终被y轴平分？若存在，求出点T的坐标，若不存在，请说明理由．

20．设$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-1，-x），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x=-$\frac{1}{2}$．

17．

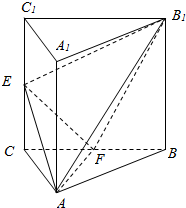如图，三棱柱ABC-A₁B₁C₁中，侧棱AA₁⊥平面ABC，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA₁=2，E，F分别是CC₁，BC的中点．
（1）求证：EF⊥平面AB₁F；
（2）求三棱锥B₁-AEF的体积；
（3）若点M是AB上一点，求|FM|+|MB₁|的最小值．

18．当a＞1时．函数y=a^f（x）与y=f（x）具有相同的的单调性；当0＜a＜1时．函数y=a^f（x）与y=f（x）具有相反的的单调性．

试题分类