题目内容
设点P的坐标为(4,3),双曲线C的方程为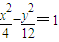 ,F是双曲线C的左焦点,若M是双曲线C上使
,F是双曲线C的左焦点,若M是双曲线C上使 取得最小值的点,则点M的坐标是( )
取得最小值的点,则点M的坐标是( )A.(
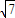 ,3)
,3)B.(2,0)
C.(
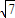 ,±3)
,±3)D.(
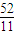 ,0)
,0)
【答案】分析:过点M作左准线l:x=-1的垂线MB,交l于B,由双曲线的第二定义知 ,
, 的最小值为点P到左准线l:x=-1的距离.由此能够求出P点坐标.
的最小值为点P到左准线l:x=-1的距离.由此能够求出P点坐标.
解答:解:过点M作左准线l:x=-1的垂线MB,交l于B,
则 ,∴
,∴ ,
,
 的最小值为点P到左准线l:x=-1的距离.
的最小值为点P到左准线l:x=-1的距离.
过点P垂直于左准线l:x=-1的直线方程是y=3,
解方程组 ,(x>0)得x=
,(x>0)得x= ,y=3,即P(
,y=3,即P( ).
).
故选A.
点评:本题考查双曲线的简单性质,解题时要认真审题,仔细解答.
 ,
, 的最小值为点P到左准线l:x=-1的距离.由此能够求出P点坐标.
的最小值为点P到左准线l:x=-1的距离.由此能够求出P点坐标.解答:解:过点M作左准线l:x=-1的垂线MB,交l于B,
则
 ,∴
,∴ ,
, 的最小值为点P到左准线l:x=-1的距离.
的最小值为点P到左准线l:x=-1的距离.过点P垂直于左准线l:x=-1的直线方程是y=3,
解方程组
 ,(x>0)得x=
,(x>0)得x= ,y=3,即P(
,y=3,即P( ).
).故选A.
点评:本题考查双曲线的简单性质,解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设点P的坐标为(4,3),双曲线C的方程为
-
=1,F是双曲线C的左焦点,若M是双曲线C上使|PM|+
|MF|取得最小值的点,则点M的坐标是( )
| x2 |
| 4 |
| y2 |
| 12 |
| 1 |
| 2 |
A、(
| ||
| B、(2,0) | ||
C、(
| ||
D、(
|
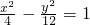 ,F是双曲线C的左焦点,若M是双曲线C上使
,F是双曲线C的左焦点,若M是双曲线C上使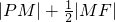 取得最小值的点,则点M的坐标是
取得最小值的点,则点M的坐标是 ,3)
,3)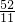 ,0)
,0)