Question

若实数x，y满足不等式组

x+2y-5≥0 2x+y-7≥0 x≥0，y≥0

，若x、y为整数，则3x+4y的最小值为

13

．

Answer 1

分析：由实数x，y满足不等式组

x+2y-5≥0 2x+y-7≥0 x≥0，y≥0

，作出可行域，利用角点法能求出3x+4y的最小值．

解答：解：由实数x，y满足不等式组

x+2y-5≥0 2x+y-7≥0 x≥0，y≥0

，
作出可行域：

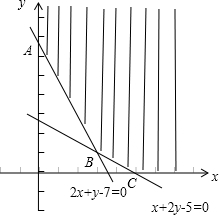
设t=3x+4y，
∵A（0，7），∴z_A=3×0+4×7=18；
解方程组

2x+y-7=0 x+2y-5=0

，得B（3，1），∴z_B=3×3+4×1=13；
∵C（5，0），∴z_C=3×5+4×0=15．
∴3x+4y的最小值为13．
故答案为：13．

点评：本题考查线性规划问题，是基础题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、找出关键点、求出最优解．