Question

(本小题满分12分)

已知函数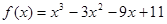

（1）写出函数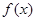的递减区间；

（2）讨论函数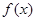的极大值或极小值，如有试写出极值；

 

Answer 1

【答案】

（1）（2）函数极大值，极小值

【解析】

试题分析：解：令，得，，

x变化时，的符号变化情况及的增减性如下表所示：

		-1		3
	+	0	-	0	+
	增	极大值	减	极小值	增

（1）由表可得函数的递减区间为

（2）由表可得，当时，函数有极大值；当时，函数有极小值

考点：函数的单调性与导数的关系；函数的极值与函数的关系。

点评：求函数的性质，常结合函数的导数来求出。