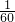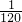题目内容
若(
-1)6的展开式中的第5项等于
,则
(a+a2+…+an)的值为( )
| a |
| 15 |
| 2 |
| lim |
| n→∞ |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
分析:由条件求出a的值,再利用等比数列的前n项和公式,求出a+a2+…+an 的值,即可得到
(a+a2+…+an)的值.
| lim |
| n→∞ |
解答:解:由题意可得
=C64 a,∴a=
.
∴a+a2+…+an=
=
=1-(
)n.
则
(a+a2+…+an)=
(1-(
)n)=1.
故选A.
| 15 |
| 2 |
| 1 |
| 2 |
∴a+a2+…+an=
| a(1-an) |
| 1-a |
| ||||
1-
|
| 1 |
| 2 |
则
| lim |
| n→∞ |
| lim |
| n→∞ |
| 1 |
| 2 |
故选A.
点评:本题考查二项展开式的通项公式,等比数列的前n项和公式,求出a+a2+…+an=1-(
)n,是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
 已知下列结论:
已知下列结论:

 A、
A、 如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是
如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是