题目内容
当圆
上一点P的旋转角为θ=
π时，点P的坐标为
|
| 2 |
| 3 |
（-2，2
）
| 3 |
（-2，2
）
．| 3 |
分析：将θ=
π代入圆的参数方程，由此即可得到点P的坐标．
| 2 |
| 3 |
解答：解：根据圆的参数方程的意义，
当圆
上一点P的旋转角为θ=
π时，点P的坐标为（4cos
，4sin
），
即（-2，2
）．
故答案为：（-2，2
）．
当圆
|
| 2 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
即（-2，2
| 3 |
故答案为：（-2，2
| 3 |
点评：本题给出圆的参数方程，求圆上旋转角为θ=
π时的点P坐标．着重考查了三角函数化简等知识，属于基础题．
| 2 |
| 3 |
练习册系列答案
相关题目
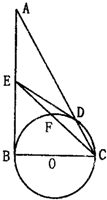（选修4-1）如图，在△ABC中，∠ABC=90°，以BC为直径的圆O交AC于点D，设E为AB的中点． 