题目内容
在一幢20m高的楼顶,测得对面一塔吊顶的仰角为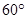 ,塔基的俯角为
,塔基的俯角为 ,那么塔吊的高是( )
,那么塔吊的高是( )
A. | B. | C. | D. |
B
解析试题分析:解:由题意,AB=20米,∠DAE=60°,∠DAC=45°,可知ABCD是正方形,有此易得CD=AD=20米,再由,∠DAE=60°,在直角三角形ADE中可求得DE= ,AD=20
,AD=20 ∴塔高为DE+CD="20+20"
∴塔高为DE+CD="20+20"  =20(
=20( +1)故选B
+1)故选B
考点:三角函数模型
点评:本题考查已知三角函数模型的应用问题,解答本题的关键是建立起符合条件的模型,然后再由三角形中的相关知识进行运算,解三角形的应用一般是求距离(长度问题,高度问题等)解题时要注意综合利用所学的知识与题设中的条件,求解三角形的边与角

练习册系列答案
相关题目
已知函数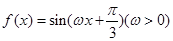 的最小正周期为
的最小正周期为 ,则该函数图象( )
,则该函数图象( )
A.关于点 对称 对称 | B.关于直线 对称 对称 |
C.关于点 对称 对称 | D.关于直线 对称 对称 |
若当 时,函数
时,函数 取得最小值,则函数
取得最小值,则函数 是( )
是( )
A.奇函数且图像关于点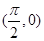 对称 对称 | B.偶函数且图像关于点 对称 对称 |
C.奇函数且图像关于直线 对称 对称 | D.偶函数且图像关于点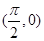 对称 对称 |
函数 =
=
 R)的图像如图所示,如果
R)的图像如图所示,如果 ,且
,且 ,则
,则
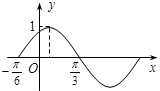
| A.1 | B. |
C. | D. |
为得到函数 的图象,只需将函数
的图象,只需将函数 的图像( )
的图像( )
A.向左平移 个长度单位 个长度单位 | B.向右平移 个长度单位 个长度单位 |
C.向左平移 个长度单位 个长度单位 | D.向右平移 个长度单位 个长度单位 |
tan300°+ 的值是
的值是
A.1+ | B.1- | C.-1- | D.-1+ |
已知 ,则
,则 =( )
=( )
A. | B.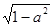 | C. | D.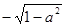 |
为了得到函数 的图像,需要把函数
的图像,需要把函数 图像上的所有点( )
图像上的所有点( )
A.横坐标缩短到原来的 倍,再向右平移 倍,再向右平移 个单位长度 个单位长度 |
B.横坐标伸长到原来的 倍,再向右平移 倍,再向右平移 个单位长度 个单位长度 |
C.横坐标缩短到原来的 倍,再向左平移 倍,再向左平移 个单位长度 个单位长度 |
D.横坐标伸长到原来的 倍,再向左平移 倍,再向左平移 个单位长度 个单位长度 |
 (其中
(其中 )的图象如图所示,为了得
)的图象如图所示,为了得 的图像,则只要将
的图像,则只要将 的图像 ( )
的图像 ( ) 
 个单位长度 B.向右平移
个单位长度 B.向右平移 个单位长度
个单位长度