题目内容

已知函数y=asin（2x+
π
6
）+b在x∈[0，
π
2
]上的值域为[-5，1]，求a、b的值．
分析：根据三角函数的定义域和值域列出方程组进行求解．
解答：解：∵x∈[0，
π
2
]
∴2x+
π
6
∈[
π
6
，
7π
6
]
∴sin（2x+
π
6
） 的最大值为sin
π
2
=1
            最小值为sin
7π
6
=-
1
2

当a≥0时
a+b=1
-
a
2
+b=-5
   解得：
a=4
b=-3

当a＜0时
a+b=-5
-
a
2
+b=1
     解得：
a=-4
b=-1
点评：考查了三角函数定义域和值域的内容，属于中档题．
练习册系列答案
相关题目
已知函数y=Asin（ωx+φ），在同一周期内，当x=
π
12
时，取最大值y=2，当x=
7π
12
时，取得最小值y=-2，那么函数的解析式为（　　）
A、y=
1
2
sin（x+
π
3
）
B、y=2sin（2x+
π
3
）
C、y=2sin（
x
2
-
π
6
）
D、y=2sin（2x+
π
6
）
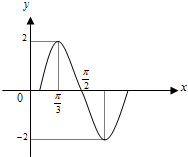精英家教网已知函数y=Asin（ωx+∅）（A＞0，ω＞0，-π≤∅≤π）一个周期的图象（如图），则这个函数的一个解析式为（　　）
A、y=2sin(
3
2
x+
π
2
)
B、y=2sin(3x+
π
6
)
C、y=2sin(3x-
π
6
)
D、y=2sin(3x-
π
2
)
已知函数y=Asin(ωx+?)+B(A＞0，ω＞0，|?|＜
π
2
)的周期为T，在一个周期内的图象如图所示，则φ=
-
π
6
-
π
6
．
已知函数y=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的一部分图象如图所示，则（　　）
已知函数y=Asin（ωx+∅）+k的最大值为4，最小值为0，最小正周期是
π
2
，在x∈[
π
24
，
π
12
]上单调递增，则下列符合条件的解析式是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网