题目内容
4.函数$y=\sqrt{1-tan({x-\frac{π}{4}})}$的定义域为( )| A. | $(kπ,kπ+\frac{π}{4}],k∈Z$ | B. | $(kπ,kπ+\frac{π}{2}],k∈Z$ | C. | $(kπ-\frac{π}{4},kπ+\frac{π}{2}],k∈Z$ | D. | $(kπ-\frac{π}{4},kπ],k∈Z$ |
分析 根据二次根式的性质以及正切函数的性质求出函数的定义域即可.
解答 解:由题意得:1-tan(x-$\frac{π}{4}$)≥0,
故tan(x-$\frac{π}{4}$)≤1,
故kπ-$\frac{π}{2}$<x-$\frac{π}{4}$≤kπ+$\frac{π}{4}$,
解得:x∈(kπ-$\frac{π}{4}$,kπ+$\frac{π}{2}$],k∈z,
故选:C.
点评 本题考查了求函数的定义域问题,考查三角函数的性质,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.函数$y=tan({x-\frac{π}{4}})$的单调递增区间为( )
| A. | $({kπ-\frac{π}{2},kπ+\frac{π}{2}})({k∈Z})$ | B. | (kπ,kπ+π)(k∈Z) | C. | $({kπ-\frac{3π}{4},kπ+\frac{π}{4}})({k∈Z})$ | D. | $({kπ-\frac{π}{4},kπ+\frac{3π}{4}})({k∈Z})$ |
13.用反证法证明:“若x>0,y>0,x+y>2,求证x,y中至少有一个大于1”时,反设正确的是( )
| A. | 假设x,y都不大于1 | B. | 假设x,y都小于1 | ||
| C. | 假设x,y至多有一个大于1 | D. | 假设x,y至多有两个大于1 |
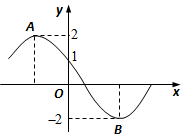 如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=2.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(-1)=2.