题目内容
已知函数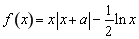 .
.
(Ⅰ)若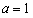 ,求
,求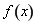 在点
在点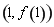 处的切线方程;
处的切线方程;
(Ⅱ)求函数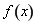 的极值点.
的极值点.
【答案】
(Ⅰ)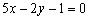 ;(Ⅱ)当
;(Ⅱ)当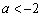 时,
时,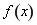 的极小值点为
的极小值点为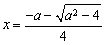 和
和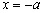 ,极大值点为
,极大值点为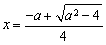 ;当
;当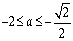 时,
时,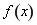 的极小值点为
的极小值点为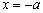 ;当
;当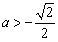 时,
时,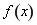 的极小值点为
的极小值点为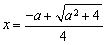 .
.
【解析】
试题分析:(Ⅰ)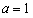 时,
时,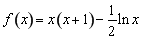 ,先求切线斜率
,先求切线斜率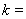
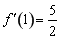 ,又切点为
,又切点为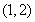 ,利用直线的点斜式方程求出直线方程;(Ⅱ)极值点即定义域内导数为0的根,且在其两侧导数值异号,首先求得定义域为
,利用直线的点斜式方程求出直线方程;(Ⅱ)极值点即定义域内导数为0的根,且在其两侧导数值异号,首先求得定义域为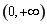 ,再去绝对号,分为
,再去绝对号,分为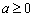 和
和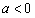 两种情况,其次分别求
两种情况,其次分别求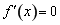 的根并与定义域比较,将定义域外的舍去,并结合图象判断其两侧导数符号,进而求极值点;
的根并与定义域比较,将定义域外的舍去,并结合图象判断其两侧导数符号,进而求极值点;
试题解析: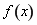 的定义域为
的定义域为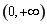 .
.
(Ⅰ)若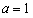 ,则
,则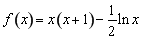 ,此时
,此时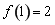 .因为
.因为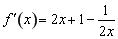 ,所以
,所以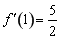 ,所以切线方程为
,所以切线方程为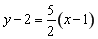 ,即
,即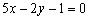 .
.
(Ⅱ)由于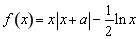 ,
,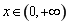 .
.
⑴ 当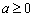 时,
时,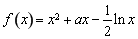 ,
,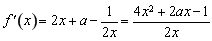 ,
,
令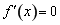 ,得
,得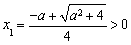 ,
,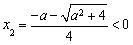 (舍去),
(舍去),
且当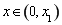 时,
时,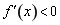 ;当
;当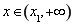 时,
时,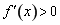 ,
,
所以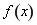 在
在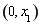 上单调递减,在
上单调递减,在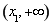 上单调递增,
上单调递增,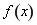 的极小值点为
的极小值点为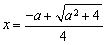 .
.
⑵ 当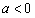 时,
时,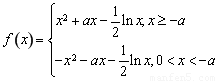 .
.
① 当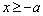 时,
时,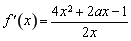 ,令
,令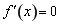 ,得
,得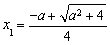 ,
,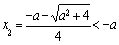 (舍去).
(舍去).
若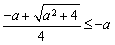 ,即
,即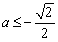 ,则
,则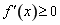 ,所以
,所以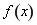 在
在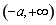 上单调递增;
上单调递增;
若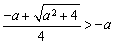 ,即
,即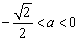 , 则当
, 则当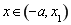 时,
时,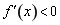 ;当
;当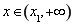 时,
时,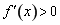 ,所以
,所以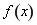 在区间
在区间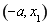 上是单调递减,在
上是单调递减,在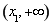 上单调递增,
上单调递增,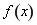 的极小值点为
的极小值点为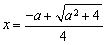 .
.
② 当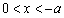 时,
时,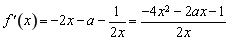 .
.
令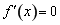 ,得
,得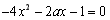 ,记
,记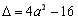 ,
,
若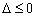 ,即
,即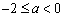 时,
时,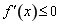 ,所以
,所以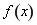 在
在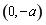 上单调递减;
上单调递减;
若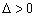 ,即
,即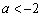 时,则由
时,则由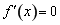 得
得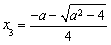 ,
,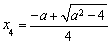 且
且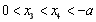 ,
,
当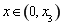 时,
时,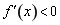 ;当
;当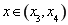 时,
时,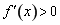 ;当
;当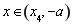 时,
时,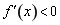 ,
,
所以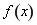 在区间
在区间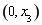 上单调递减,在
上单调递减,在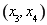 上单调递增;在
上单调递增;在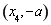 上单调递减.
上单调递减.
综上所述,当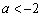 时,
时,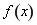 的极小值点为
的极小值点为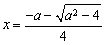 和
和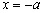 ,极大值点为
,极大值点为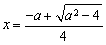 ;
;
当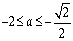 时,
时,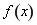 的极小值点为
的极小值点为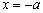 ;
;
当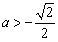 时,
时,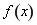 的极小值点为
的极小值点为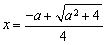 .
.
考点:1、导数的几何意义;2、函数的极值和最值;3、导数在函数单调性上的应用.

练习册系列答案
相关题目
 ,
,
 与曲线
与曲线 在它们的交点(1,c)处具有公共切线,求
在它们的交点(1,c)处具有公共切线,求 ,
,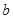 的值;
的值; ,
, 时,若函数
时,若函数 在区间[
在区间[ ,2]上的最大值为28,求
,2]上的最大值为28,求 ,
, 在
在 上的最大值为
上的最大值为 ,求实数
,求实数 的值;
的值; ,都有
,都有 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,对任意给定的正实数
,对任意给定的正实数 上是否存在两点
上是否存在两点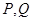 ,使得
,使得 是以
是以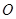 (
( 轴上?请说明理由。
轴上?请说明理由。