题目内容
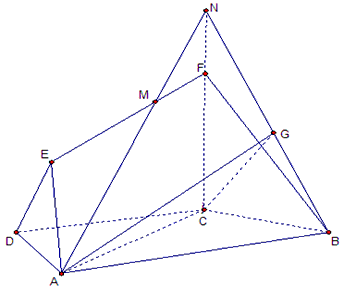
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1,
(1)求证:BC⊥平面ACFE;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围。
(1)求证:BC⊥平面ACFE;
(2)求二面角A-BF-C的平面角的余弦值;
(3)若点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围。
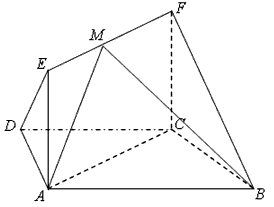
| (1)证明:在梯形ABCD中, ∵AB∥CD,AD=DC=CB=1,∠ABC=60°, ∴AB=2, ∴ 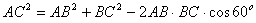 =3, ∴ 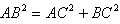 , ,∴BC⊥AC, ∵平面ACEF⊥平面ABCD, 平面ACFE∩平面ABCD=AC, 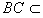 平面ABCD, 平面ABCD,∴BC⊥平面ACFE。 |
|
| (2)解:取FB中点为G,连结AG、CG, ∵ 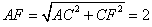 , , ∴AB=AF, ∴AG⊥FB, ∵CF=CB=1, ∴CG⊥FB, ∴∠AGC=θ, ∵BC⊥CF, ∴ 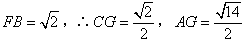 , ,∴ 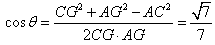 ; ;(3)解:由(2)知, ①当M与F重合时, 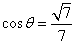 ; ;②当M与E重合时,过B作BN∥CF, 且使BN=CF,连结EN、FN, 则平面 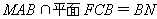 , ,∵BC⊥CF,又∵AC⊥CF, ∴CF⊥平面ABC, ∴BN⊥平面ABC, ∴∠ABC=θ, ∴θ=60°, ∴ 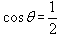 ; ;③当M与E、F都不重合时, 令 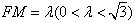 , ,延长AM交CF的延长线于N,连结BN, ∴N在平面MAB与平面FCB的交线上, ∵B在平面MAB与平面FCB的交线上, ∴平面MAB∩平面FCB=BN, 过C作CH⊥NB交NB于H ,连结AH, 由(Ⅰ)知,AC⊥BC, 又∵AC⊥CN, ∴AC⊥平面NCB, ∴AC⊥NB, 又∵CH⊥NB,AC∩CH=C, ∴NB⊥平面ACH, ∴AH⊥NB, ∴∠AHC=θ, 在△NAC中, 可求得NC= 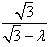 , ,从而,在△NCB中, 可求得CH= 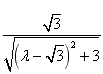 , , ∵∠ACH=90°, ∴AH= 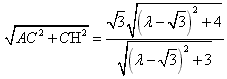 , , ∴ 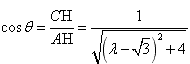 , , ∵ 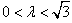 , , ∴ 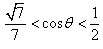 , ,综上得 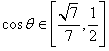 。 。 |
 |

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
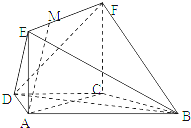 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=a,.∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上.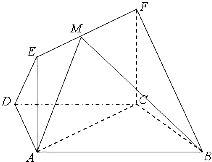 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.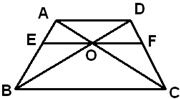 如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF=
如图,在梯形ABCD中,AD∥BC,BD与AC相交于O,过O的直线分别交AB、CD于E、F,且EF∥BC,若AD=12,BC=20,则EF= 如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出
如图,在梯形ABCD中,对角线AC和BD交于点O,E、F分别是AC和BD的中点,分别写出 如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.
如图,在梯形△ABCD中,AB∥CD,AD=DC-=CB=1,么ABC-60.,四边形ACFE为矩形,平面ACFE上平面ABCD,CF=1.