题目内容
某年级的一次信息技术成绩近似服从于正态分布N（70，100），如果规定低于60分为不及格，不低于90分为优秀，那么成绩不及格的学生约占多少？成绩优秀的学生约占多少？（参考数据：P（μ-σ＜ξ＜μ+σ）=0.6826，P（μ-2σ＜ξ＜μ+2σ）=0.9544）
【答案】分析：先由题意得：μ=70，σ=10．再利用正态分布的意义和3σ原则：P（μ-σ＜ξ＜μ+σ）=0.6826，P（μ-2σ＜ξ＜μ+2σ）=0.9544，计算即可．
解答：解：因为由题意得：μ=70，σ=10，
P（μ-σ＜ξ＜μ+σ）=0.6826，P（μ-2σ＜ξ＜μ+2σ）=0.9544
（1）
=0.1587，
（2）
．
答：成绩不及格的学生约占15.87%，成绩优秀的学生约占2.28%．
点评：本题主要考查了连续型随机变量的概率分布正态分布的意义和应用，正态分布曲线的对称性，转化化归的思想方法，属基础题．
解答：解：因为由题意得：μ=70，σ=10，
P（μ-σ＜ξ＜μ+σ）=0.6826，P（μ-2σ＜ξ＜μ+2σ）=0.9544
（1）
=0.1587，（2）
．答：成绩不及格的学生约占15.87%，成绩优秀的学生约占2.28%．
点评：本题主要考查了连续型随机变量的概率分布正态分布的意义和应用，正态分布曲线的对称性，转化化归的思想方法，属基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
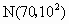，如果规定低于60分为不及格，求：
