Question

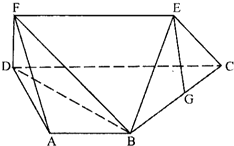（2011•温州二模）如图多面体ABCDEF，AB∥CD∥EF  FD丄面ABCD BC=AD=AB=2，EF=3，DC=4，FD=1
（I）若G是BC的中点，求证：EG∥平面AFD；
（II）求直线EC与平面BDF所成角的正切值．

Answer 1

分析：（I）取AD的中点H，先利用平行公理及梯形中位线定理证明四边形EFGH为平行四边形，再利用线面平行的判定定理证明EG∥平面AFD
（II）先作出这个线面角的平面角，即过F作FM∥EC，过M作MN⊥BD，垂足为N，连接FN，再利用线面垂直的判定定理证明
MN⊥面BDF，从而证明∠MFN就是EC与面BDF所成的角，最后在直角三角形中计算此角的正切值即可

解答：解：（I）证明：取AD的中点H，连接FH，GH，因为GH∥DC∥EF，GH=EF=3，所以四边形EFGH为平行四边形
故有EG∥FH，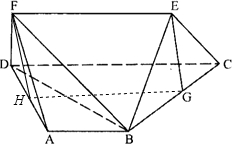
又EG?平面ADE，FH?平面ADE
所以EG∥平面AFD
（II）解：过F作FM∥EC，过M作MN⊥BD，垂足为N，连接FN，
因为FD⊥面ABCD，所以FD⊥MN，BD∩FD=D
所以MN⊥面BDF，
所以∠MFN就是EC与面BDF所成的角
过B作BO⊥DC，垂足为O，
因为四边形ABCD是等腰梯形
所以OC=1，BO=

3

，DO=3，DM=1，BD=2

3

因为△DBO∽△DMN
所以MN=

DM×BO

BD

=

1

2

在Rt△FDM中，FM=

2

所以在Rt△FNM中，FN=

7

2

所以tan∠MFN=

MN

FN

=

7

7

故直线EC与平面BDF所成角的正切值为

7

7

点评：本题综合考查了线面平行的判定，平行公理，线面垂直的判定，以及线面角的作法、证法、算法，体现了将空间问题转化为平面问题的思想方法，解题时要辨清线面关系，避免想当然思想和运算错误