题目内容
已知二次函数k≤1图象经过坐标原点,其导函数为f′(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上;又b1=1,cn=
(an+2),且1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn,对任意n∈N*都成立,
(1)求数列{an},{bn}的通项公式;
(2)求数列{cn•bn}的前n项和Tn;
(3)求证:(i)ln(x+1)<(x>0);(ii)
<
(n∈N*,n≥2).
| 1 |
| 3 |
(1)求数列{an},{bn}的通项公式;
(2)求数列{cn•bn}的前n项和Tn;
(3)求证:(i)ln(x+1)<(x>0);(ii)
| n |
 |
| i=2 |
| lnai |
| ai2 |
| 2n2-n-1 |
| 4(n+1) |
分析:(1)设二次函数f(x)=ax2+bx并求出f'(x),由题意求出a和b,代入求出f(x),由(n,Sn)在y=f(x)上求出Sn,由Sn与an的关系能求出an,再由题意求出cn,令n=n-1(n≥2)代入再两式作差求出bn,需要验证n=1时是否成立,不成立再用分段函数的形式表示出来;
(2)由(1)求出cn•bn,根据特点利用错位相减法求出Tn;
(3)(i)构造函数g(x)=x-ln(x+1)(x>0),再求导数判断此函数单调性,求出函数的值域即得证;
(ii)根据(i)构造lnn<n-1(n≥2),再变形、赋值、放缩得:
<1-
,代入
化简后,再进一步放缩利用裂项相消法求和即可.
(2)由(1)求出cn•bn,根据特点利用错位相减法求出Tn;
(3)(i)构造函数g(x)=x-ln(x+1)(x>0),再求导数判断此函数单调性,求出函数的值域即得证;
(ii)根据(i)构造lnn<n-1(n≥2),再变形、赋值、放缩得:
| lnn2 |
| n2 |
| 1 |
| n2 |
| n |
 |
| i=2 |
| lni |
| i2 |
解答:解:(1)设二次函数f(x)=ax2+bx,f'(x)=2ax+b,
∴2a=6b=-2,则f(x)=3x2-2x,
∵(n,Sn)在y=3x2-2x上,∴Sn=3n2-2n.
当n≥2时an=Sn-Sn-1
=3n2-2n-3(n-1)2+2(n-1)=6n-5
又n=1时a1=3-2=1=6×1-5符合,
∴an=6n-5,
则cn=
(an+2)=
=2n-1,
由b1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn得,
b1+2a2+22b3+…+2n-2bn-1+2n-1bn=2n-1 ①,
令n=n-1(n≥2)代入上式得,
b1+2a2+22b3+…+2n-2bn-1+2n-2bn-1=2n-3 ②,
①-②得,2n-1bn=2,即bn=22-n(n≥2),
又∵b1=1不满足上式,
∴bn=
,
(3)由(2)得,cn•bn=
,
∴Tn=1+3+5×2-1+7×2-2+…+(2n-1)×22-n ③,
Tn=
+3×2-1+5×2-2+7×2-3+…+(2n-1)×21-n ④,
③-④得,
Tn=
+2(2-1+2-2+…+22-n)-(2n-1)×21-n
=
+2×
-(2n-1)×21-n=
-(2n+3)×21-n,
则Tn=11-(2n+3)×22-n,
(3)(i)设g(x)=x-ln(x+1)(x>0),则g′(x)=1-
=
>0,
∴g(x)在(0,+∞)上是增函数,
∴g(x)>g(0)=0,即x-ln(x+1)>0,
故ln(x+1)<x(x>0);
(ii)∵ln(x+1)<x(x>0),
当n∈N*,n≥2时,令n=n-1代入上式得:
lnn<n-1,即
<
=1-
,
令n=n2代入上式得,
<1-
,∴
<
(1-
)
则
=
+
+…+
<
(1-
+1-
+…+1-
)
=
[(n-1)-(
+
+…+
)]<
[(n-1)-(
+
+…+
)]
=
[(n-1)-(
-
+
-
+…+
-
)]
=
[(n-1)-(
-
)]=
[(n-1)-
]=
,
故结论成立.
∴2a=6b=-2,则f(x)=3x2-2x,
∵(n,Sn)在y=3x2-2x上,∴Sn=3n2-2n.
当n≥2时an=Sn-Sn-1
=3n2-2n-3(n-1)2+2(n-1)=6n-5
又n=1时a1=3-2=1=6×1-5符合,
∴an=6n-5,
则cn=
| 1 |
| 3 |
| 6n-3 |
| 3 |
由b1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn得,
b1+2a2+22b3+…+2n-2bn-1+2n-1bn=2n-1 ①,
令n=n-1(n≥2)代入上式得,
b1+2a2+22b3+…+2n-2bn-1+2n-2bn-1=2n-3 ②,
①-②得,2n-1bn=2,即bn=22-n(n≥2),
又∵b1=1不满足上式,
∴bn=
|
(3)由(2)得,cn•bn=
|
∴Tn=1+3+5×2-1+7×2-2+…+(2n-1)×22-n ③,
| 1 |
| 2 |
| 1 |
| 2 |
③-④得,
| 1 |
| 2 |
| 7 |
| 2 |
=
| 7 |
| 2 |
| ||||
1-
|
| 11 |
| 2 |
则Tn=11-(2n+3)×22-n,
(3)(i)设g(x)=x-ln(x+1)(x>0),则g′(x)=1-
| 1 |
| x+1 |
| x |
| x+1 |
∴g(x)在(0,+∞)上是增函数,
∴g(x)>g(0)=0,即x-ln(x+1)>0,
故ln(x+1)<x(x>0);
(ii)∵ln(x+1)<x(x>0),
当n∈N*,n≥2时,令n=n-1代入上式得:
lnn<n-1,即
| lnn |
| n |
| n-1 |
| n |
| 1 |
| n |
令n=n2代入上式得,
| lnn2 |
| n2 |
| 1 |
| n2 |
| lnn |
| n2 |
| 1 |
| 2 |
| 1 |
| n2 |
则
| n |
 |
| i=2 |
| lni |
| i2 |
| ln2 |
| 22 |
| ln3 |
| 32 |
| lnn2 |
| n2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
=
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
| n-1 |
| 2(n+1) |
| 2n2-n-1 |
| 4(n+1) |
故结论成立.
点评:本题是数列与不等式的综合,涉及了数列的前n项和与项之间的转化,错位相减法和错位相减法求和,综合性强,难度较大.多次用到放缩法和构造函数法,解题时要认真审题,会用分析法找思路,特别是放缩的目标,解决此题需要较强的逻辑思维能力和计算能力.

练习册系列答案
相关题目
 (an+2),且1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn,对任意n∈N*都成立,
(an+2),且1+2a2+22b3+…+2n-2bn-1+2n-1bn=cn,对任意n∈N*都成立,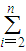
 <
< (n∈N*,n≥2).
(n∈N*,n≥2).