题目内容
已知α,β是不重合的平面,m,n是不重合的直线,下列命题正确的序号为
①m∥n,n∥α⇒m∥α;
②m⊥α,m⊥β⇒α∥β;
③α∩β=n,m∥α,m∥β⇒m∥n;
④α⊥β,m⊥α,n⊥β⇒m⊥n.
①m∥n,n∥α⇒m∥α;
②m⊥α,m⊥β⇒α∥β;
③α∩β=n,m∥α,m∥β⇒m∥n;
④α⊥β,m⊥α,n⊥β⇒m⊥n.
分析:根据线面平行的判定定理来判断①是否正确;
根据垂直于同一直线的两个平面平行来判断②是否正确;
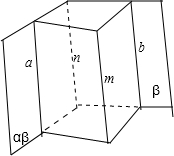
借助图形,如图过m作两个相交平面,分别与α,β相交于直线a,b,可证a∥b,从而可证a∥n,进而可证m∥n,由此判断③是否正确;
取直线m、n的方向向量
,
,根据α⊥β,则
⊥
,可判断④是否正确.
根据垂直于同一直线的两个平面平行来判断②是否正确;
借助图形,如图过m作两个相交平面,分别与α,β相交于直线a,b,可证a∥b,从而可证a∥n,进而可证m∥n,由此判断③是否正确;
取直线m、n的方向向量
| m |
| n |
| m |
| n |
解答:解:对①,缺少条件m?α,∴①错误;
对②,根据垂直于同一直线的两个平面平行,∴②正确;
对③,如图过m作两个相交平面,分别与α,β相交于直线a,b,可证m∥a,m∥b,∴a∥b,
可证a∥β,α∩β=n,∴a∥n,∴m∥n,故③正确;
对④,∵m⊥α,n⊥β,α⊥β,∴
⊥
,∴m⊥n,故④正确.
故答案是②③④.
对②,根据垂直于同一直线的两个平面平行,∴②正确;
对③,如图过m作两个相交平面,分别与α,β相交于直线a,b,可证m∥a,m∥b,∴a∥b,
可证a∥β,α∩β=n,∴a∥n,∴m∥n,故③正确;
对④,∵m⊥α,n⊥β,α⊥β,∴
| m |
| n |
故答案是②③④.

点评:本题考查了线线,线面平行、垂直关系的判断,熟练掌握线面平行、垂直的判定与性质定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目