题目内容
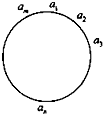 如图所示:m个实a1a2…,am(m≥3且m∈N)依次按顺时针方向围成一个圆圈.
如图所示:m个实a1a2…,am(m≥3且m∈N)依次按顺时针方向围成一个圆圈.(1)已知a1=1且an+1=an+
| 1 | m(n+1) |
(2)设圆圈上按顺时针方向任意相邻的三个数ap、aq、ar均满足:aq=λap+ar(λ>0),求证:a1=a2=…=am.
分析:(1)由a1=1且an+1=an+
(n∈N,n<m),推导出am=2-
,由此能求出m的最小值.
(2)由aq=λap+(1-λ)ar(λ>0),得λ(ap-aq)=(1-λ)(ar-aq),当λ=1时,a1=a2=…=am成立.当λ≠1时,ar-aq=
(aq-ap),由此利用分类讨论思想能够证明a1=a2=…=am.
| 1 |
| m(n+1) |
| 1 |
| m |
(2)由aq=λap+(1-λ)ar(λ>0),得λ(ap-aq)=(1-λ)(ar-aq),当λ=1时,a1=a2=…=am成立.当λ≠1时,ar-aq=
| λ |
| 1-λ |
解答:解:(1)∵a1=1且an+1=an+
(n∈N,n<m),
∴am=a1+
+
+…+
=1+1-
+
-
+…+
-
=2-
,
∵an>1.99(m∈N+),
∴
<0.01,∴m>100,
于是,m的最小值为101.
(2)∵aq=λap+(1-λ)ar(λ>0),
∴λ(ap-aq)=(1-λ)(ar-aq),
当λ=1时,a1=a2=…=am成立.
当λ≠1时,ar-aq=
(aq-ap),
则数列{an-an-1}(2≤n≤m)是等比数列,于是:
am-am-1=(a2-a1)(
)m-2,又a1-am=
(am-am-1),
a2-a1=
(a1-am),
∴a2-a1=(
)m(a2-a1),
所以
=1,或a2-a1=0.
若a2-a1=0,则a1=a2=…=am.
若
=1,则λ=
,
此时数列{an}(1≤n≤m)为等差数列,设公差为d,
则am=a1+(m-1)d,am-1=a1+(m-2)d,
又am=
,∴d=0,
∴a1=a2=…=am.
综上所述:a1=a2=…=am.
| 1 |
| m(n+1) |
∴am=a1+
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| (m-1)m |
=1+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| m-1 |
| 1 |
| m |
| 1 |
| m |
∵an>1.99(m∈N+),
∴
| 1 |
| m |
于是,m的最小值为101.
(2)∵aq=λap+(1-λ)ar(λ>0),
∴λ(ap-aq)=(1-λ)(ar-aq),
当λ=1时,a1=a2=…=am成立.
当λ≠1时,ar-aq=
| λ |
| 1-λ |
则数列{an-an-1}(2≤n≤m)是等比数列,于是:
am-am-1=(a2-a1)(
| λ |
| 1-λ |
| λ |
| 1-λ |
a2-a1=
| λ |
| 1-λ |
∴a2-a1=(
| λ |
| 1-λ |
所以
| λ |
| 1-λ |
若a2-a1=0,则a1=a2=…=am.
若
| λ |
| 1-λ |
| 1 |
| 2 |
此时数列{an}(1≤n≤m)为等差数列,设公差为d,
则am=a1+(m-1)d,am-1=a1+(m-2)d,
又am=
| am-1+a1 |
| 2 |
∴a1=a2=…=am.
综上所述:a1=a2=…=am.
点评:本题考查数列与不等式的综合应用,考查推理谁能力和计算应用能力,综合性强,难度大,是高考的重点.解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 如图所示:m个实a1a2…,am(m≥3且m∈N)依次按顺时针方向围成一个圆圈.
如图所示:m个实a1a2…,am(m≥3且m∈N)依次按顺时针方向围成一个圆圈.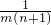 (n∈N,n<m),若am>1.99恒成立,求m的最小值;
(n∈N,n<m),若am>1.99恒成立,求m的最小值;