题目内容
四面体ABCD的外接球球心在CD上,且CD=2,AB=| 3 |
分析:根据球心到四个顶点距离相等可推断出O为CD的中点,且OA=OB=OC=OD,进而在△A0B中,利用余弦定理求得cos∠AOB的值,则∠AOB可求,进而根据弧长的计算方法求得答案.
解答:解:球心到四个顶点距离相等,故球心O在CD中点,则OA=OB=OC=OD=1
再由AB=
,在△A0B中,利用余弦定理cos∠AOB=
=-
则∠AOB=120°,则弧AB=
•2π•1=
故答案为:
再由AB=
| 3 |
| OA2+OB2-AB2 |
| 2•OA•OB |
| 1 |
| 2 |
则∠AOB=120°,则弧AB=
| 120° |
| 360° |
| 2π |
| 3 |
故答案为:
| 2π |
| 3 |
点评:本题主要考查了余弦定理的应用.四面体外接球的性质等.考查了学生观察分析和基本的运算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
在矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
正四面体ABCD的外接球球心为O,E为BC的中点,则二面A-BO-E的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
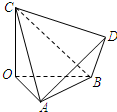 如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.
如图,四面体OABC的三条棱OA,OB,OC两两垂直,OA=OB=2,OC=3,D为四面体OABC外一点.给出下列命题.