题目内容
已知函数f（n）=
，且an=f（n）+f（n+1），则a1+a2+a3+…+a100等于 ．
【答案】分析：先求出通项公式an，然后两项一组，求数列的前100项的和
解答：解：∵an=f（n）+f（n+1）
∴由已知条件知，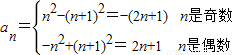
∴
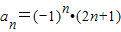
∴an+an+1=2（n是奇数）
∴a1+a2+a3+…+a100=（a1+a2）+（a3+a4）+…+（a99+a100）=2+2+2+…+2=100
故答案为：100
点评：本题考查数列的通项公式的求法和前n项和的求法，须注意对通项公式和问题的灵活变形．属简单题
解答：解：∵an=f（n）+f（n+1）
∴由已知条件知，
∴
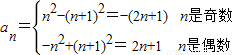
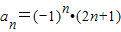
∴an+an+1=2（n是奇数）
∴a1+a2+a3+…+a100=（a1+a2）+（a3+a4）+…+（a99+a100）=2+2+2+…+2=100
故答案为：100
点评：本题考查数列的通项公式的求法和前n项和的求法，须注意对通项公式和问题的灵活变形．属简单题
练习册系列答案
相关题目
已知函数f（n）=n2cos（nπ），且an=f（n）+f（n+1），则a1+a2+a3+…+a100=（ ）
| A、0 | B、-100 | C、100 | D、10200 |