题目内容
已知函数f(x)=| lim |
| n→∞ |
| ||||
2n+
|
(1)f(x)的定义域,并画出图象;
(2)求
| lim |
| x→-2- |
| lim |
| x→-2+ |
| lim |
| x→-2 |
分析:(1)讨论当|x|>2,|x|<2,当x=2时和当x=-2时,求出函数的极限即可得到f(x)的定义域,画出图象;
(2)分别求出x→-2-,x→2+时函数的极限,得到两者不相等,所以
f(x)不存在.
(2)分别求出x→-2-,x→2+时函数的极限,得到两者不相等,所以
| lim |
| x→-2 |
解答:解:(1)当|x|>2时,
=
=-1;
当|x|<2时,
=
=1;
当x=2时,
=0;
当x=-2时,
不存在.
∴f(x)=
∴f(x)的定义域为{x|x<-2或x=2或x>2}.如图所示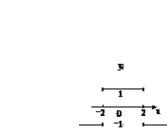
(2)∵
f(x)=-1,
f(x)=1.
∴
f(x)不存在.
| lim |
| n→∞ |
| ||
| 2n+xn |
| lim |
| n→∞ |
(
| ||
(
|
当|x|<2时,
| lim |
| n→∞ |
| 2n-xn |
| 2n+xn |
| lim |
| n→∞ |
1-(
| ||
1+(
|
当x=2时,
| lim |
| n→∞ |
| 2n-xn |
| 2n+xn |
当x=-2时,
| lim |
| n→∞ |
| 2n-xn |
| 2n+xn |
∴f(x)=
|
∴f(x)的定义域为{x|x<-2或x=2或x>2}.如图所示

(2)∵
| lim |
| x→-2- |
| lim |
| x→-2+ |
∴
| lim |
| x→-2 |
点评:考查学生会求函数的左极限及右极限并会判断函数极限的存在性.会求不同的取值范围函数的极限.

练习册系列答案
相关题目