题目内容
【题目】已知正项数列{an}的前n项和为Sn ， 且a1=1，an+12=Sn+1+Sn ．
（1）求{an}的通项公式；
（2）设bn=a2n﹣1
， 求数列{bn}的前n项和Tn ．
【答案】解：（1）∵an+12=Sn+1+Sn ， ∴当n≥2时，
=Sn+Sn﹣1 ， 可得an+12﹣=an+1+an ，
∵an+1+an＞0，∴an+1﹣an=1．
∴数列{an}是等差数列，首项为1，公差为1．
∴an=1+（n﹣1）×1=n．
（2）bn=a2n﹣1
=（2n﹣1）2n ．
∴数列{bn}的前n项和Tn=2+3×22+5×23+…+（2n﹣1）2n ．
∴2Tn=22+3×23+…+（2n﹣3）2n+（2n﹣1）2n+1 ，
∴﹣Tn=2+2（22+23+…+2n）﹣（2n﹣1）2n+1=
﹣2﹣（2n﹣1）2n+1=（3﹣2n）2n+1﹣6，
【解析】（1）由an+12=Sn+1+Sn ， 利用递推关系可得an+12﹣=an+1+an ， 由于an+1+an＞0，可得an+1﹣an=1．再利用等差数列的通项公式即可得出；
（2）利用“错位相减法”与等比数列的前n项和公式即可得出．
【考点精析】认真审题，首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系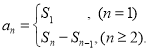
)，还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键．
科学实验活动册系列答案
【题目】近年来共享单车在我国主要城市发展迅速．目前市场上有多种类型的共享单车，有关部门对其中三种共享单车方式（M方式、Y方式、F方式）进行统计（统计对象年龄在15～55岁），相关数据如表1，表2所示． 三种共享单车方式人群年龄比例（表1）
方式 | M | Y | F |
[15，25） | 25% | 20% | 35% |
[25，35） | 50% | 55% | 25% |
[35，45） | 20% | 20% | 20% |
[45，55] | 5% | a% | 20% |
不同性别选择共享单车种类情况统计（表2）
性别 | 男 | 女 |
1 | 20% | 50% |
2 | 35% | 40% |
3 | 45% | 10% |
（Ⅰ）根据表1估算出使用Y共享单车方式人群的平均年龄；
（Ⅱ）若从统计对象中随机选取男女各一人，试估计男性使用共享单车种类数大于女性使用共享单车种类数的概率；
（Ⅲ）现有一个年龄在25～35岁之间的共享单车用户，那么他使用Y方式出行的概率最大，使用F方式出行的概率最小，试问此结论是否正确？（只需写出结论）
