题目内容
已知函数f(x)=sin(wx+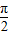 )(w>0),其图象上相邻的两个最低点间的距离为2π.
)(w>0),其图象上相邻的两个最低点间的距离为2π.(1)求ω的值及f(x)
(2)若a∈(-
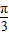 ,
,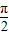 ),f(a+
),f(a+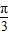 )=
)= ,求sin(2a+
,求sin(2a+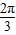 )的值.
)的值.
【答案】分析:(1)由函数图象上相邻的两个最低点间的距离为2π,可得其周期为2π,进而可求w,可得解析式;
(2)由题意可得cos(a+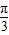 )=
)= ,通过三角函数公式可求其正弦值,而sin(2a+
,通过三角函数公式可求其正弦值,而sin(2a+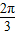 )=2sin(
)=2sin(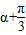 )cos(
)cos(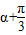 ),代值可求.
),代值可求.
解答:解:(1)因为函数f(x)=sin(wx+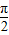 )(w>0),图象上相邻的两个最低点间的距离为2π.
)(w>0),图象上相邻的两个最低点间的距离为2π.
所以函数的周期为2π,由T=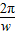 =2π,可得w=1,
=2π,可得w=1,
故f(x)=sin(x+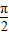 )=cosx
)=cosx
(2)由(1)可知f(x)=cosx,可得cos(a+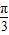 )=
)= ,又a∈(-
,又a∈(-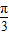 ,
,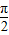 ),所以
),所以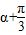 ∈(0,
∈(0,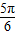 )
)
所以sin(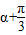 )=
)=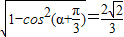 ,
,
所以sin(2α+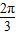 )=2sin(
)=2sin(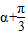 )cos(
)cos(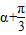 )=
)=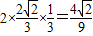
点评:本题为三角函数的基本运算,把图象问题转化为式子的运算和交点整体运用是解决问题的关键,属中档题.
(2)由题意可得cos(a+
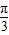 )=
)= ,通过三角函数公式可求其正弦值,而sin(2a+
,通过三角函数公式可求其正弦值,而sin(2a+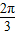 )=2sin(
)=2sin(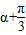 )cos(
)cos(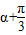 ),代值可求.
),代值可求.解答:解:(1)因为函数f(x)=sin(wx+
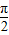 )(w>0),图象上相邻的两个最低点间的距离为2π.
)(w>0),图象上相邻的两个最低点间的距离为2π.所以函数的周期为2π,由T=
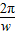 =2π,可得w=1,
=2π,可得w=1,故f(x)=sin(x+
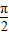 )=cosx
)=cosx(2)由(1)可知f(x)=cosx,可得cos(a+
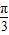 )=
)= ,又a∈(-
,又a∈(-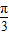 ,
,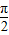 ),所以
),所以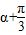 ∈(0,
∈(0,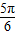 )
)所以sin(
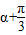 )=
)=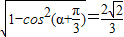 ,
,所以sin(2α+
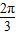 )=2sin(
)=2sin(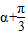 )cos(
)cos(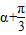 )=
)=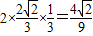
点评:本题为三角函数的基本运算,把图象问题转化为式子的运算和交点整体运用是解决问题的关键,属中档题.

练习册系列答案
相关题目
