题目内容
设a1+a2+…+an=n,其中a1,a2,…,an都是正数，求证：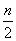
+…+
+…+
.
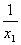证明：运用基本不等式1+ai4≥2ai2,∴左边≤.
由柯西不等式(x1+x2+…+xn)(++…+
)≥n2,
可得［(1+a1)+(1+a2)+…+(1+an)］(
+…+
)≥n2.
又∵a1+a2+…+an=n，
∴
+…+
≥
.
综上所知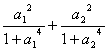
+…+
+…+
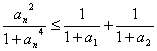练习册系列答案
天天向上口算本系列答案
相关题目
天天向上口算本系列答案题目内容
设a1+a2+…+an=n,其中a1,a2,…,an都是正数，求证：+…++…+.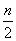
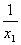证明：运用基本不等式1+ai4≥2ai2,∴左边≤.
由柯西不等式(x1+x2+…+xn)(++…+)≥n2,
可得［(1+a1)+(1+a2)+…+(1+an)］(+…+)≥n2.
又∵a1+a2+…+an=n，
∴+…+≥.
综上所知+…++…+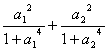
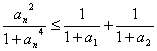天天向上口算本系列答案
的值为( )
B.
C.
D.1
+
的最小值为( )
B.
C.
D.2
+
的最小值为( )
B.
C.
D.2