题目内容
已知F1,F2为椭圆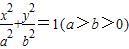 的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率为
的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率为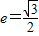 ,则椭圆的方程为 .
,则椭圆的方程为 .
【答案】分析:由于过F2作椭圆的弦AB,△AF1B的周长为16,可求a的值,由离心率可求c的值,根据几何量之间的关系可求b的值,从而可得椭圆方程.
解答:解:根据椭圆的定义,△AF1B的周长为16可知,4a=16,∴a=4,∵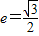 ,∴
,∴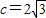 ,∴b=2,∴椭圆的方程为
,∴b=2,∴椭圆的方程为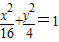 ,
,
故答案为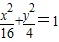
点评:本题主要考查椭圆的标准方程与几何性质,属于基础题.
解答:解:根据椭圆的定义,△AF1B的周长为16可知,4a=16,∴a=4,∵
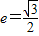 ,∴
,∴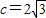 ,∴b=2,∴椭圆的方程为
,∴b=2,∴椭圆的方程为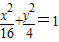 ,
,故答案为
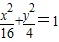
点评:本题主要考查椭圆的标准方程与几何性质,属于基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
已知F1,F2为椭圆
+
=1(a>b>0)的两个焦点,过F2作椭圆的弦AB,若△AF1B的周长为16,椭圆的离心率e=
,则椭圆的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|