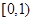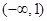题目内容
对实数 和
和 ,定义运算“
,定义运算“ ”:
”: .设函数
.设函数 ,
, .若函数
.若函数 的图象与
的图象与 轴恰有两个公共点,则实数
轴恰有两个公共点,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
B
解析试题分析:结合已知条件可知, ,因此可知,
,因此可知,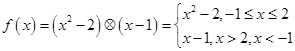 ,那么结合二次函数图像和一次函数图像可知,要使得函数
,那么结合二次函数图像和一次函数图像可知,要使得函数 的图象与
的图象与 轴恰有两个公共点,则转化为
轴恰有两个公共点,则转化为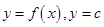 的两个函数的交点有两个即可,那么利用常函数的平移法可知参数
的两个函数的交点有两个即可,那么利用常函数的平移法可知参数 的取值范围是
的取值范围是 ,选B.
,选B.
考点:本试题考查了函数的图像与坐标轴的交点问题。
点评:解决该试题的关键是根据新定义,得到函数的解析式,然后利用分段函数的图像与性质来得到满足题意的参数的取值范围,熟悉二次函数一次函数图像,是前提,属于中档题。

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
下列说法中
① 若定义在R上的函数 满足
满足 ,则6为函数
,则6为函数 的周期;
的周期;
② 若对于任意 ,不等式
,不等式 恒成立,则
恒成立,则 ;
;
③ 定义:“若函数 对于任意
对于任意 R,都存在正常数
R,都存在正常数 ,使
,使 恒成立,则称函数
恒成立,则称函数 为有界泛函.”由该定义可知,函数
为有界泛函.”由该定义可知,函数 为有界泛函;
为有界泛函;
④对于函数 设
设 ,
, ,…,
,…, (
( 且
且 ),令集合
),令集合 ,则集合
,则集合 为空集.正确的个数为
为空集.正确的个数为
| A.1个 | B.2个 | C.3个 | D.4个 |
由表格中的数据可以判定方程 的一个零点所在的区间是
的一个零点所在的区间是 ,则
,则 的值为
的值为
 | -1 | 0 | 1 | 2 | 3 |
 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
 | 1 | 2 | 3 | 4 | 5 |
设函数 在
在 上的导函数为
上的导函数为 ,
, 在
在 上的导函数为
上的导函数为 ,若在
,若在 上,
上, 恒成立,则称函数
恒成立,则称函数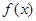 在
在 上为“凸函数”.已知当
上为“凸函数”.已知当 时,
时, 在
在 上是“凸函数”.则
上是“凸函数”.则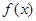 在
在 上 ( )
上 ( )
| A.既有极大值,也有极小值 | B.既有极大值,也有最小值 |
| C.有极大值,没有极小值 | D.没有极大值,也没有极小值 |
对于函数 ,若存在
,若存在 ,使
,使 成立,则称
成立,则称 为
为 的不动点. 已知函数
的不动点. 已知函数 ,若对任意实数b,函数
,若对任意实数b,函数 恒有两个相异的不动点,则实数
恒有两个相异的不动点,则实数 的取值范围是 ( )
的取值范围是 ( )
| A.(0,1) | B.(1,+∞) | C.[0,1) | D.以上都不对 |
 在
在 上既是奇函数,又为减函数. 若
上既是奇函数,又为减函数. 若 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
 ( )
( )




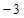


 ,的大致图象是
,的大致图象是
 ,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是
,则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是